Desafío 57. Triángulo inscrito y triángulo circunscrito I.  

En un triángulo de área A inscribir un triángulo de área Ai tal que: 

 

Caso 1º Ai =1/4A, A1=A2=A3 

 

Caso 2º Ai= 1/3A, A1=A2=A3 

 

Caso 3º Ai=1/2A, A1=A2=A3 

 

Siendo A1, A2 y A3 las áreas de los triángulos “sobrantes” 

 

4º Crear archivo GeoGebra que pueda ser válido para la comprobación o comprobaciones 

 

 

En un triángulo de área A circunscribir un triángulo de área Ac tal que: 

 

Caso 1º Ac =4A, A1=A2=A3 

 

Caso 2º Ac= 3A, A1=A2=A3 

 

Caso 3º Ac=2A, A1=A2=A3 

 

Siendo A1, A2 y A3 las áreas de los triángulos “añadidos” 

 

4º Crear archivo GeoGebra que pueda ser válido para la comprobación o comprobaciones 

 

Solución.  

Me he limitado al caso del triángulo circunscrito. Creo que el otro caso se resolvería similarmente. Para el 

triángulo circunscrito, he hecho los tres casos juntos, usando un factor k que puede valer 2, 3 ó 4 según el 

caso. Es decir, he resuelto el caso general Ac = k*A. 

 

Tanto la solución, como el geogebra, son válidos para cualquier valor de k entre 1 y 4. Para k=1, la solución 

es  trivial, puesto que el triángulo de partida y el circunscrito coinciden. Para k=4, hay una única solución 

que  consiste en girar 180º el  triángulo original  sobre el punto medio de  cada  lado, obteniendo  los  tres 

triángulos añadidos de igual área al original, que junto a este, componen el triángulo circunscrito. 

 

Para cualquier valor de k entre 1 y 3, se obtienen dos soluciones bastante diferentes. 

 

Supongo que Sebas colgará los geogebra en el blog. No obstante, yo lo colgaré también en este sitio: 

 

https://sites.google.com/site/solucionescongeogebra 

   

Resultados (triángulo circunscrito).  

Caso k=1.5 

 

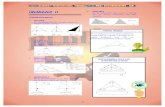
Empecemos por un caso que no se pedía: k=1.5. Es decir, se trata de hallar, para el triángulo del enunciado 

(pintado en azul en la figura), el triángulo circunscrito que cumpla: 

 

Ac = k *A, con k=1.5 en este caso 

A1=A2=A3, siendo estas las áreas de los triángulos "añadidos". 

 

Obtenemos dos soluciones: el triángulo rojo de vértices V1, V2, V3 y el triángulo verde de vértices W1, W2, 

W3.  Estas  corresponden  a  las  dos  soluciones  de  la  ecuación  de  segundo  grado  del  parámetro  t  que  se 

explica en el apartado "Construcción del triángulo circunscrito".  

 

Ambos triángulos tienen los vértices en el triángulo trazado en línea discontinua en la figura, resultante de 

aplicar una homotecia al triángulo de partida, con factor k (en este caso 1.5) y centro en el baricentro (esto 

se demuestra en el apartado "Construcción del triángulo circunscrito"). 

 

Los  lados L1', L2' y L3' del triángulo homotético distan de  los correspondientes  lados paralelos L1, L2 y L3 

del triángulo de partida (en trazo azul continuo) en estas cantidades: 

 

H1 = 2/3 A (k‐1) / L1,   H2 = 2/3 A (k‐1) / L2,   H3 = 2/3 A (k‐1) / L3 

 

   

Caso k= 2. 

 

Pasemos al  caso k=2, uno de  los pedidos en el desafío. El  triángulo de partida es el mismo. El  triángulo 

homotético es más grande,  lo que permite que el área de  los triángulos añadidos, así como el de  las dos 

soluciones (en rojo y verde) crezca. 

 

 

 

La solución "roja" de esta figura corresponde al enunciado del desafío. 

   

 

Caso k=2.5. 

 

Para k=2.5, nada nuevo que comentar. 

 

  

   

Caso k=3. 

 

Para k=3, los lados de las dos soluciones posibles son paralelos. 

 

  

Caso k=3.95. 

 

Para k=3.95 cambio  la escala porque el triángulo homotético se hace muy grande. Se observa que  las dos 

soluciones se van aproximando. 

 

 

Caso k= 4. 

 

Finalmente, para k=4,  las dos soluciones coinciden. Cada  triángulo añadido es el  resultado de girar el de 

partida  respecto  al  punto medio  de  cada  lado. Nos  quedan  4  triángulos  semejantes  que  conforman  el 

circunscrito que también es semejante. 

 

  

Para k>4 no hay solución. 

   

Evolución de las soluciones con k. 

 

En la siguiente figura se representan, para k recorrida de 1 a 4 en pasos de 0.5, los rastros dejados por las 

dos soluciones. Para k=1 ambas coinciden con el triángulo original. A medida que crece k, el triángulo verde 

"gira" a la izquierda y el rojo a la derecha (cambiando de forma y tamaño), hasta volver a coincidir para k=4. 

Por ejemplo: 

El vértice W1 del triángulo verde que empieza cerca de Q' con k cercano a 1 se desplaza hacia 

abajo por el lado L1' al aumentar k. Para el triángulo rojo es el vértice V1 el que empieza en el lado 

L1', pero cerca de O' y desplazándose hacia arriba conforme k se incrementa. 

 

Amos vértices confluyen en el centro del lado L1' para k=4. 

 

 

Pero esto lo veréis mejor en el Geogebra. 

 

   

Construcción del triángulo circunscrito  

Usaremos un sistema de coordenadas tal que el triángulo A (en azul) tenga con un vértice O en (0,0), otro 

vértice P en el semieje X positivo y el tercer vértice Q en el semi plano Y>0. Llamaremos L1 al otro lado OQ, 

L2 al lado PQ y L3 al lado OP. De este modo los triángulos A1, A2, A3 del enunciado apoyan cada uno en el 

lado con el mismo subíndice. 

 

 Solucionaremos esta parte del desafío buscando la solución de un caso general: 

 

Ac = k *A, A1=A2=A3 

 

Esto da la solución para los tres casos asignando a k los valores 4, 3 y 2. 

 

Caso 1º Ac =4A, A1=A2=A3 

Caso 2º Ac= 3A, A1=A2=A3 

Caso 3º Ac=2A, A1=A2=A3 

 

   

Relación de la altura de los triángulos añadidos con k. 

 

El área del triángulo circunscrito (el rojo) se puede expresar como: 

 

Ac = A + A1 + A2 + A3 

 

Y dado que Ac=k*A, y que además A1=A2=A3, podemos escribir: 

 

k A = A + 3 A1  

A1 = A2=A3 = A (k‐1) / 3 

 

Por otra parte, podemos expresar el área de cada triángulo añadido en función de su base, que sería el lado 

correspondiente, y su altura:  

 

A1 = L1 * H1 /2,   A2 = L2 * H2 /2,   A3 = L3 * H3 /2 

 

Lo que nos lleva a concluir que la altura de cada triángulo añadido solo depende del área A del triángulo de 

partida y del parámetro k: 

  

H1 = 2/3 A (k‐1) / L1,   H2 = 2/3 A (k‐1) / L2,   H3 = 2/3 A (k‐1) / L3 

Esto nos determina, para el lado L1 del triángulo de partida (azul), una recta paralela a una distancia H1, en 

la que sabemos que tiene que situarse el vértice del triángulo circunscrito. Lo mismo sucede con los lados 

L2 y L3, con paralelas a distancia H2 y H3 respectivamente. En  la figura se muestra  la recta L1' paralela al 

lado L1 y separada de esta una distancia H1. El vértice    tiene que estar situado sobre esta recta para que 

el área A1 valga lo que tiene que valer. 

 

Las tres rectas paralelas a los lados constituyen un triángulo semejante al azul de partida. La cuestión ahora 

será obtener la expresión de esas tres rectas, para lo cual tenemos que saber donde se sitúa exactamente 

el triángulo semejante en trazo discontinuo. 

   

El triángulo exterior es una homotecia respecto al baricentro con factor k. 

 

Partiremos de  suponer que efectivamente el  triángulo exterior es una homotecia  respecto al baricentro  

(punto donde se cruzan las medianas) del triángulo original con factor k. Calcularemos las distancias H1, H2 

y H3  que  resultan  entre  el  triángulo  de  partida  y  el  homotético.  Si  estas  coinciden  con  las  esperadas, 

quedará demostrado, puesto que solo puede haber un triángulo que lo cumpla. 

La figura siguiente corresponde a un valor de k=2.5 para no confundirnos (el caso del enunciado es para k=2 

y nos puede conducir a error al haber distancias iguales por ser k=2, pero que no es posible generalizar). Se 

han etiquetado como   O', P' y Q' a  los vértices del triángulo exterior semejante. Se han trazado  las rectas 

que  unen O  con O',  P  con  P'  y Q  con Q'.  Como  estamos  suponiendo  que  el  triángulo  exterior  es  una 

homotecia respecto al baricentro,  las tres rectas se tienen que  juntar en él. El baricentro está etiquetado 

como Z. 

 

Nos fijamos en el triángulo OPZ. Si Z es el baricentro del triángulo OPQ, su distancia al lado L3 (el segmento 

OP) debe ser un tercio de la altura del triángulo de partida en azul (distancia de Q a la recta que contiene a 

O y P). Por tanto el área del triángulo OPZ es un tercio del área del triángulo OPQ, es decir  lo que hemos 

llamado A. Esto nos permite escribir: 

D = Distancia Z a segmento OP 

Area OPZ = A/3 = L3 * D / 2 

D = 2/3 A / L3 

Igualmente, el área del  triángulo O'P'Z  será un  tercio del área del  triángulo O'P'Q'. Puesto que estamos 

suponiendo que el triángulo exterior es una homotecia del de partida por un factor k, su área será A*k^2. 

Por tanto el área de O'P'Z será un tercio de esa cantidad. Pero además, ese área es el producto de la base 

L3' por  la altura partido por 2. La base L3' será k*L3, puesto que el triángulo exterior tiene ese factor de 

escala respecto al original. La altura será D más la distancia de la recta OP a la recta O'P'. Esa distancia es la 

que hemos llamado anteriormente H3. 

Área O'P'Z' = A*k^2 / 3 = (k *L3) * (D+H3) / 2 

Dividiendo entre k tenemos: 

A*k / 3 = L3 * (D+H3) / 2 

D+H3 = 2/3 A*k / L3 

Restando a esta última expresión la que habíamos hallado al ver el triángulo OPZ: 

D+H3 = 2/3 A*k / L3 

D = 2/3 A / L3 

H3 = 2/3 (k‐1) / L3 

Hemos  supuesto que el  triángulo de  trazo discontinuo  es una homotecia  respecto  al baricentro  con un 

factor k del triángulo de partida, y nos sale que  las distancias entre  los  lados de ambos triángulos son  las 

que  precisábamos.  Es  decir,  el  triángulo  que  buscamos  es  el  homotético  respecto  al  baricentro  que 

estábamos suponiendo. 

 

Empezamos a calcular coordenadas. 

 

Hasta ahora que sabemos que los vértices del triángulo circunscrito V1, V2, V3 están sobre los lados de un 

triángulo semejante al de partida resultante de realizar una homotecia de este respecto al baricentro por 

un factor k. 

Para  avanzar,  empezaremos  por  calcular  las  coordenadas  de  las  rectas  en  las  que  están  estos  vértices. 

Primeramente recordemos el sistema de coordenadas: 

Origen en O:  0,0  

Punto P en semieje x positivo:  , 0  

Punto Q en semiplano Y positivo:  ,  

 

Seguiremos calculando  las coordenadas del baricentro. Cuando  lo hice, desconocía que  la distancia de un 

baricentro a un lado es un tercio de la altura correspondiente. Teniendo en cuenta eso el cálculo podría ser 

mucho más  sencillo. He dejado  el  cálculo original que  si  se quiere,  se puede  tomar  también  como una 

demostración de que el baricentro está a un  tercio de  la altura de cada  lado. Para no perder el hilo del 

desafío, el cálculo de las coordenadas del baricentro está separado en el anexo al final de la solución, como 

he hecho con otros cálculos pesados.  

 

El resultado es simple, y obviamente solo depende de las coordenadas de P y Q que definen el triángulo de 

partida: 

 

 

3,3

 

   

Continuaremos realizando el cálculo de las ecuaciones de las rectas de los lados L1', L2' y L3' del triángulo 

en trazo azul discontinuo homotético del de partida en trazo azul continuo. Recordemos, como se ve en la 

figura, que sobre estas rectas se apoyan los vértices V1, V2, V3 del triángulo circunscrito que constituye la 

solución. Las coordenadas de O', P' y Q' así como las ecuaciones de las rectas ya no dependen solo de P y de 

Q, sino que también estará involucrado el factor k que determina el caso del desafío (k=4,3,2). 

 

Los cálculos están realizados en el anexo. Los resultados son: 

′  1

3,

1

3 

   2 

3,

1

3  

     2 

3,  1 2

3 

Recta que contiene al lado L1': 

  1

3  

Recta que contiene al lado L2': 

2     

3   

Recta que contiene al lado L3': 

1

3 

 

   

Estrategia que sigue. 

 

Hasta  ahora,  sabemos  que  los  vértices  del  triángulo  circunscrito  V1,  V2,  V3  están  sobre  el  triángulo 

homotético O' P' Q'. Con ello, cumplen  la  relación entre  las áreas. Lo difícil es situar  los  tres vértices de 

modo que pasen por los puntos O, P y Q. 

La estrategia que seguiremos es situar un punto M3 en el lado L3', en un punto cualquiera. Trazaremos la 

recta  que  pasa  por M3  y  por  P,  e  intersecionaremos  esta  con  el  lado  L2'.  Al  punto  de  intersección  le 

llamaremos M2. Desde M2, trazaremos la recta que pasa por Q y la interseccionaremos con el lado L1', en 

un punto que llamaremos M1. Desde M1, trazaremos la recta que pasa por O y la interseccionaremos con 

L3', en un punto que llamaremos M4. 

Si acertamos a situar el primer punto en la posición adecuada, el punto final M4 de este proceso coincidirá 

con M3. En este caso, M1, M2 y M3 formarán un triángulo que cumple  las condiciones: circunscrito al de 

partida y con las áreas de los triángulos añadidos adecuadas. 

Desde  luego, colocando M3 a voleo tenemos pocas posibilidades de acertar. Lo más probable es que nos 

pase algo como esto: 

 

Lo que haremos es considerar la coordenada X de M3 como un parámetro, y veremos a que coordenada de 

M4  conduce.  Ambos  puntos, M3  y M4,  tienen  la misma  coordenada  Y  puesto  que  están  en  una  recta 

horizontal. 

Sobre el  resultado que obtengamos,  impondremos que  la  coordenada X  sea  también  la misma. Eso nos 

dará una ecuación en la que la única incógnita es la coordenada X de M3. Su solución, o soluciones, nos da 

la respuesta al desafío. 

   

Desarrollo de la estrategia. 

 

Partiremos de un punto M3 cualquiera de la recta del lado L3', que vendrá dado por estas coordenadas: 

,1

3 

Donde t es la coordenada X que tomaremos como un parámetro. El resto de términos que intervendrán en 

las formulas son constantes para un problema dado:  las coordenadas de  los puntos P y Q que definen el 

triángulo de partida, y el factor k que define el caso (4, 3 ó 2). 

El proceso a seguir en resumen es hallar   como intersección de la recta que pasa por   y por P con la 

del lado L2', a continuación   como intersección de la recta que pasa por   y por Q con la recta del lado 

L1' y finalmente el punto   como intersección de la recta  y O con recta del lado L3'. 

Nada más  empezar  a  intentarlo,  la  primera  en  la  frente.  La  ecuación  de  la  primera  recta  que  hay  que 

calcular  (la  que  une    y  por  P)  es  un  chorizo  respetable.  Conforme  se  iban  avanzando  pasos,  las 

expresiones de los puntos y rectas se iban complicando cada vez más. 

 

Así que mi opción ha sido la siguiente: cada vez que se complica la expresión de la ecuación de una recta o 

las  coordenadas  de  un  punto,  uso  unas  variables  auxiliares A, B,  C  (con  subíndices)  para  escribirlas del 

modo más  sencillo posible.  Pero  estas  variables  tienen que  ser  "constantes",  es decir, depender de  los 

datos de partida (P,Q,k), pero no del parámetro t que es una incógnita. 

 

He separado los cálculos en el anexo, de modo que sea más fácil seguir el hilo de la solución. En la siguiente 

página se resume es las expresiones de los puntos M3, M2, M1, M4 y las ecuaciones de las rectas que los 

unen, juntos con las definiciones de las variables auxiliares  

   

Resultados de los cálculos. 

 

Expresión de la recta o punto Definición de las variables auxiliares

Recta que pasa por M3 y P: 

   

 

1 /3 

 

1 /3 

Punto M2:   ,

  

 

 

/   /   

/   

/   

 

 

Recta que pasa por M2 y Q:  

 

 

 

    

 

  

  

 

  

  

 

Punto M1: 

 ,

  

 

  

   

  

  

 

 

Recta que pasa por M1 yO:  

   

    

 

 

Punto M4:  

1  

3   ,

1

3 

 

 

   

Resolviendo el desafío 

 

Recapitulemos: 

 

Hemos demostrado que para un triángulo de partida cualquiera, definido por las posiciones de sus 

vértices O, P, Q, y para un  factor k que determina el  caso del desafío,  los vértices del  triángulo 

circunscrito  pedido  de  área  Ac=k*A  tienen  que  estar  en  triángulo  homotético  del  de  partida 

respecto a su baricentro con un factor k. 

 

Hemos partido de un punto M3 en el lado L3' del triángulo homotético que es horizontal respecto 

al sistema de coordenadas que hemos definido, y hemos hallado sucesivamente las expresiones de 

los puntos M2 sobre el lado L2', M1 sobre el lado L1' y M4 sobre el lado L3' a los que se llega por 

intersecciones de  las  rectas que pasan por cada punto y uno de  los del partida con  los  lados del 

triángulo homotético. Estas expresiones dependen de un gran número de variables auxiliares, pero 

tienen un valor constante para un triángulo de partida y un k dados. 

 

    

Lo que nos queda es ver en que condiciones, el punto M3 de partida y el punto M4 final coinciden. Cuando 

lo hagan, habremos encontrado la solución al desafío. 

 

El  punto M3  tiene  una  coordenada  X  que  hemos  llamado  t.  El  punto  final M4  viene  dado  por  esta 

expresión: 

 

1  

3   ,

1

3 

 

Lo que haremos es forzar que la coordenadas X de ambos puntos sean iguales (la coordenada Y siempre lo 

fue). Es decir: 

 

1  

3    

 

Esto conduce a una ecuación de segundo grado para t: 

 

1 1   3    3     

 

3    3  1   1 0 

 

Recordando que todas las variables involucradas dependen en última instancia de las coordenadas de P, Q 

y de  k,  las dos posibles  soluciones para  t nos  conducen  a  los dos posibles  triángulos que  solucionan  el 

desafío. 

 

Dicho así, parece cuestión de fé y desde luego no queda como solución muy elegante. Lo suyo sería haber 

llegado a fórmulas analíticas para t, pero los desarrollos que salen son indigeribles. 

 

   

Contenido del geogebra. 

 

Lo bueno es que este desafío pide  la  comprobación en Geogebra, y ahí no hay problemas para  realizar 

cálculos reiterativos. Así pués, en el Geogebra está calculado lo siguiente: 

 

Los vértices O, P y Q del triángulo de partida. O es el punto fijo (0,0), P se puede trasladar por el eje 

X y Q mover libremente. 

 

El triángulo de partida en trazo azul continuo (denominado TriInt en Geogebra). 

 

Un deslizador para el parámetro k, entre 1 y 4. 

 

Las variables A1, etc. que dependen de las coordenadas de P y Q y del factor k. 

 

El triángulo homotético al de partida, definido por  las rectas L1', L2', L3' (trazo azul discontinuo) y 

los vértices O', P', Q'. 

 

Las soluciones t1 y t2 de  la ecuación de segundo grado que sale al  imponer que en el proceso de 

construcción el punto M3 y M4 coincidan: 

 

3    3  1   1 0 

 

El triángulo TriExt1 en rojo corrrespondiente a  la primera solución y el triángulo TriExt2 en verde 

correspondiente a la segunda, así como sus vértices V1, V2, V3 y W1, W2, W3. 

 

Para jugar con el Geogebra, deslizad el punto P a lo largo del eje X (oculto) o el Q libremente para cambiar 

el  triángulo  de  partida. Moviendo  el  deslizador  k  elegís  el  caso.  Tras  cada  cambio  de  alguno  de  estos 

parámetros (posición de P, de Q o valor de k), se reconstruye toda la figura: el triángulo homotético en azul 

discontinuo y las soluciones en verde y rojo. 

 

Los vértices ocultos en naranja M1, M2, M3 y M4 y las rectas Cons1, Cons2, Cons3 reproducen el proceso 

de construcción seguido para resolver el desafío. 

   

ANEXO: Cálculos pesados.  

Coordenadas del baricentro del triángulo de partida: 

 

Calcularemos las coordenadas del baricentro, por intersección de las dos medianas más sencillas.  

Ecuación mediana por ( ,  ) y por  / ,  

2

   

2   

2 

2   

2    

2   2   

2 

2   

2    

2 

2   

2    

 

Ecuación mediana por ( / , /   y por  ,  

22

2

 2

 

2 2  

2 

2 2  2 2    

2 

2  2  2  2  2    

2 

2  2  2    

 2  2    

 

Intersectando las rectas obtenemos el baricentro: 

2 

2   

2  

 2  2    

2   2 

2   

2  2    

2  2  2  2    2     

  3     

 

3 

 

 2  2 

 

3

3   

 3  2 

2 

 3  2   3  

 

 

3,3

 

   

Ecuaciones de las rectas L1', L2', L3' del triángulo exterior homotético al de partida  

 

Realizamos la homotecia respecto al baricentro con factor de escala k del origen, P y Q para obtener los 

puntos O', P', Q'. Estos forman el triángulo homotético en trazo azul discontinuo de lados L1', L2', L3'. 

′  1

3,

1

3 

 

3,3

 2 

3,3

   2 

3,

1

3  

 

3,3

 2 

3,2 

3

     2 

3,  1 2

3 

Las ecuaciones de la recta que contiene al lado L1' se puede calcular teniendo en cuenta que pasa por O' y 

tiene la dirección (Qx,Qy):  

1

3   

  1

3 

  1

3  

La recta del lado L2' pasa por P' y tiene dirección (Qx‐Px,Qy): 

1

3   

   2 

3 

1    2 

3   

     2 

3   

2     

3   

La recta del lado L3' pasa por O' y es paralela al eje x: 

1

3 

   

Ecuación de la recta que pasa por   y P: 

 

Partiendo de las coordenadas de M3: 

 

,1

3 

La ecuación de la recta que lo une con P sería: 

 

  1

3∗  

  1

3

  1

3 

En esta ecuación, para un  triángulo  interior dado, conocemos  ,   y    , y para cada caso del desafío 

conocemos k. Por tanto lo que nos interesa es distinguir en las ecuaciones las partes dependientes de t. Así 

que reescribimos la ecuación así: 

   1 /3 1 /3

 

Y usamos unas variables auxiliares para simplificarla: 

   

Donde las variables se pueden calcular como: 

  1 /3 

 

  1 /3 

 

   

Cálculo del punto M2: 

 

El punto M2 es la intersección de la recta calculada en el apartado anterior con la recta que contiene al lado 

L2': 

2     

3   

     

 2     

3 

 

Resolvemos el sistema de dos ecuaciones: 

       

     

       

    

/   /   /   

/  

   

/   /   

/   

/   

        

  

   

 

  

   

Recta que pasa por M2 y Q: 

 

 ,

  

 

    

    

        

 

                  

El término independiente es: 

        

          

        

  

Introduciremos unas variables 

  

  

 

La ecuación de la recta queda así: 

 

 

 

    

  

  

 

   

Calculo del punto M1 

 

M1 es la intersección de la recta anterior con la del lado L1: 

  1

3    

  1

3  

 

Resolvemos el sistema 

 

 

 

      

           

    

      

  

 

  

   

  

  

    

    

 

 

 

   

Ecuación de la recta que pasa por M1 y por el origen. 

 

 ,

  

 

 

    

 

    

Cálculo del punto M4 

 

Es la intersección de la recta anterior con la del lado L1': 

1

3 

Resolvemos el sistema: 

   

  

1

3 

 1  

3    

1  

3   ,

1

3