UNIVERSIDAD NACIONAL DE SAN MARTIN

FACULTAD DE INGENIERIA CIVILESCUELA ACADEMIC PROFESIONAL DE INGENIERIA CIVIL

TRABAJO ENCARGADO N 04SISTEMAS VIBRATORIOS

La vibracin es el movimiento oscilatorio de partculas y de cuerpos rgidos y elsticos, bajo la accin de fuerzas fluctuantes. Estas fuerzas fluctuantes pueden ser inherentes a los sistemas, o pueden aplicarse exteriormente a dichos sistemas. Los problemas de vibracin se presentan en muchos aspectos de la ingeniera, tales como la vibracin de la maquinaria que opera a altas velocidades, aeroplanos y vehculos espaciales, edificios, torres, puentes, instrumentos dinmicos de medicin, y vibracin aislada, pata mencionar unos cuantos; en esta seccin consideraremos solamente la vibracin de una partcula con un solo grado de libertad.Primero definiremos algunos trminos bsicos relativos a la vibracin usando un modelo vibratorio simple, consistente de una masa y un resorte, como se indica en la figura.

FIGURA

La masa se designa por m o por su peso W, y el resorte por K la figura 8-12b indica que el resorte se alarga al unirse al l el peso, siendo el alargamiento. Supongamos tambin que no hay movimiento en el caso b. en la parte c de la figura, la oscilacin ascendente y descendente de la masa se indica mediante las flechas y las posiciones extremas se indican con lneas discontinuas. No nos importara saber como comienza la oscilacin; puede deberse a una fuerza perturbadora impulsiva o a un desplazamiento inicial.

Con este modelo sencillo definimos los trminos siguientes:a) K, la constante de resorte, es la fuerza necesaria para alargar o comprimir el resorte una unidad de longitud(es decir, las unidades de k son lb/pulg, kg/cm, etc.)b) Posicin de equilibrio(o posicin neutra, o posicin central) es la posicin en la cual m esta bajo la accin de dos fuerzas iguales y opuestas, W y k , y se encuentra en equilibrio esttico.c) Posiciones extremas son las posiciones ms alejadas de la posicin de equilibrio en donde las velocidades son cero.d) Amplitud es el valor numrico del mximo desplazamiento hacia cualquier lado de la posicin de equilibrio. En la mayora de los casos las dos amplitudes son iguales.e) Desplazamiento total es la suma de las dos amplitudes.f) Movimientos peridicos son movimiento que se repiten en intervalos de movimientos iguales.g) Periodo, es el tiempo que transcurre mientras el movimiento se repite.h) Ciclo es el movimiento ejecutado durante el periodo.i) Frecuencia es el nmero de ciclos completos de movimiento, en la unidad de tiempo.j) Movimiento armnico es la forma ms simple de peridico y se representa mediante una funcin seno o coseno. Todos los movimientos armnicos son peridicos, pero no todos los movimientos peridicos son armnicos.

Usando los conceptos de los trminos bsicos anteriores, describiremos lo siguiente:

1. Frecuencia Angular. Como el movimiento armnico puede representarse por medio de la proyeccin, sobre un dimetro, de un vector giratorio, con forme se mueve alrededor de un circulo con una rapidez angular constante (fig.8-14), podemos deducir la relacin existente entre el periodo t, la frecuencia f, y la rapidez angular constante , como sigue: ya que una funcin circular se repite cada 2 rad., un ciclo de movimiento se completa cuando:

t=2 Tambin, por definicin

t = 1/ffig.

Por lo tanto, tenemos:

En donde las unidades son las ms comnmente usadas en los problemas de vibracin como:

fA tambin se le llama frecuencia angular o frecuencia circular.

2. Vibracin Libre Y Vibracin Forzada. En el caso del modelo vibratorio masa-resorte la fuerza del resorte es la que produce la vibracin. Como esta fuerza es inherente al sistema, la vibracin se llama vibracin libre. Cuando hay una fuerza aplicada exteriormente sobre la masa o el soporte, la vibracin se llama vibracin forzada. La fig 8-15 muestra varios tipos de fuerzas aplacadas: (a) fuerza senoidal, (b) fuerza peridica, (c)fuerza no peridica (d)fuerza aleatoria. En esta seccin nos ocuparemos solamente de la fuerza senoidal.

Figura 8-15

3. Resorte Equivalente(Composicin De Resortes). Cuando dos resortes se conecten en paralelo o serie podemos substituirlo por un solo resorte equivalente. El procedimiento usado para obtener este resorte equivalente se llama composicin de resortes. Para un sistema simple consistente de dos resortes conectados paralelos, tal como lo indicado en la fig. 8-16 podemos escribir.

Para n resortes se deduce que, (8-48)

Para un sistema simple consistente de dios resortes conectados en serie, tal como el indicado en la fig. 8-17, tenemos

Y para n resortes conectados en serie: ..(8-49)

4. Fuerza amortiguadora. A menudo un sistema vibratorio se sujeta a una fuerza amortiguadora, que puede deberse a un dispositivo amortiguador en el sistema o a las fuerzas de friccin que existen en todos los sistemas fsicos, o a ambas causas. Algunas veces la fuerza de friccin puede ser despreciable, en comparacin con otras fuerzas que actan en el sistema, en cuyo caso, el sistema puede considerarse amortiguado. Un tipo muy comn de amortiguamiento que desarrolla una fuerza que es proporcional y de sentido contrario a la velocidad se llama amortiguamiento viscoso. Para una velocidad v, la fuerza de amortiguamiento es cv, en donde la constante de proporcionalidad c se llama coeficiente de amortiguamiento viscoso.5. Grado de libertad. El nmero de coordenadas independientes necesarias para especificar el movimiento de un sistema es el grado de libertad del sistema si una partcula se esta en movimiento en una direccin, se dice que tiene un grado de libertad. En esta seccin consideremos la vibracin de una partcula con un grado de libertad.

Ahora ya estamos separados para tratar los problemas de vibracin.

Ecuacin General De Movimiento Para Una Partcula Vibratoria Con Un Grado De Libertad. Consideremos una partcula oscilante de masa m que esta sujeta a la accin de una fuerza de resorte, una fuerza amortiguadora y una fuerza aplicada exteriormente. Consideremos que esta partcula tiene un grado de libertad y que el movimiento vibratorio se efecta a lo largo del eje x, como se indica en la fig. 8-18(b) nos muestra el diagrama de cuerpo libre. La ecuacin de movimiento es:

En donde

, Si el resorte es lineal, el amortiguamiento es viscoso y la fuerza aplicada exteriormente es armnica. Po lo tanto

(8-50)Sean:

Entonces la ecuacin de movimiento es:

.(8-51)En esta seccin consideraremos cuatro casos de vibracin de una partcula con un grado de libertad, regida por la ecuacin general de movimiento de la ecuacin anterior.Caso 1. Vibracin libre no amortiguada. En este caso, tanto la fuerza amortiguadora como las fuerzas aplicadas exteriormente son cero, es decir

Y la ecuacin de movimiento se convierte en (8-52)La solucin de esta ecuacin diferencial lineal y homognea, es

En donde son las constantes de integracin que se determina a partir de las condiciones iniciales para t = 0, entonces Esta solucin puede escribirse como : (8-53) En donde,

En la ecuacin anterior A es la amplitud y es el ngulo de fase. Como solamente hay una partcula en movimiento y no hay amortiguacin ni fuerza aplicada exteriormente, en el angulo de fase puede escogerse arbitrariamente. Esto significa que el tiempo t = 0 puede escogerse que = 0. Aqu t = 0 sucede cuando

es decir las condiciones iniciales son: Por consiguiente El periodo de este movimiento es, ..(8-54)

Y la frecuencia es, ..(8-55)

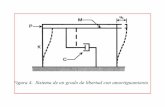
Esta es la frecuencia natural del sistema. El sistema y su movimiento se indican en la fig.

PROBLEMASPROBLEMA 21-27. Un bloque que pesa 50N est suspendido en un plano vertical por tres resortes, segn se indica en la figura. Si se desplaza 175 mm hacia arriba a partir de su posicin de equilibrio y se suelta con una velocidad hacia arriba de 3.75 m/s cuando t= 0, determinar:a. La ecuacin diferencial que rige el movimiento.b. El periodo y la amplitud de la vibracin resultante.c. La posicin del bloque en funcin del tiempo.d. El menor tiempo t1 de paso del bloque por su posicin de equilibrio.

SOLUCION: Datos: y= 175 mm= 0.175 m

m= DCL

Calculando K equivalente :

a. Calculando la ecuacin diferencial del movimiento : K

b. Calculo del periodo y la amplitud: T= T= 0.366 S

V= A= 0.28 mA= A=

c. Calculo de la posicin del bloque en funcin del tiempo:Sea la solucin de la ecuacin diferencial del movimiento: . ..

En para Y= 0.175 t= 0 En : para = 3.75 t=0 0.175 = 3.75=

Por lo tanto la ecuacin es:

d. Calculo del tiempo:De la ecuacin por partir del punto de equilibrio Y= 0.175 = 0.28

t= 0.04 s.

PROBLEMA 21-28. Una masa de 4 kg est suspendida en un plano vertical, segn la figura. Los resorte estn sometidos a traccin en todo momento y las poleas son pequeas y estn exentas de rozamiento. Si se lleva la masa a 15 mm por encima de su posicin de equilibrio y se le suelta con una velocidad de 750 mm/s hacia abajo cuando t= 0, determinar:a. La ecuacin diferencial que rige el movimiento.b. El periodo y la amplitud de la vibracin resultante.c. La posicin de la masa en funcin del tiempo.d. El menor tiempo correspondiente a velocidad nula de la masa.

Solucin: Datos: x= 15 mm= 0.015 m m= 4

Calculando K equivalente :

= +2 = +2 a. Calculando la ecuacin diferencial del movimiento: 2(

b. Calculo del periodo y la amplitud: T= T= 0.89 S

V= A= 0.1 mA= A=

c. Calculo de la posicin del bloque en funcin del tiempo:Sea la solucin de la ecuacin diferencial del movimiento: . ..

En para x= 0.015 t= 0 En : para = 0.75 t=0 0.015 = 0.75=

Por lo tanto la ecuacin es:

d. Calculo del tiempo:De la ecuacin por partir del punto de equilibrio Y= 0.015 = 0.1

t= 0.088 s.

PROBLEMA 21-41. Una rueda escalonada que pesa 90N rueda sin deslizamiento por un plano horizontal, segn se indica en la figura. Los dos resortes estn unidos a hilos arrollados de manera segura sobre el cubo central de 30cm de dimetro. Si el radio de giro del cilindro escalonado vale 225mm,escribir la ecuacin diferencial del movimiento para la posicin XG(t) del centro de masa del cilindro determinar la frecuencia y el periodo del movimiento vibratorio resultante.

SOLUCION: Haciendo DCL: Datos: ;

r1r2 K2K1

( = 1.2915 MC =

K1(3)

30

K2 Reemplazando y resolviedo tenemos:

15

PROBLEMA 21-50. Un peso de 6kg pende del cilindro del problema 21-40 segn se indica en la figura P21-50 , mediante un pasador exento de rozamiento que pasa por su centro. Escribir la ecuacin diferencial del movimiento para la posicin yg(t) del centro de masa del cilindro y determinar la frecuencia y el periodo del movimiento vibratorio resultante.

SOLUCION : Haciendo las ecuac. De equilibrio:Haciendo DCL : Fy = 0 ; mTg - T -keq = 0..1

O Mo = 0 ; Tr = keq keq = T..2

CB cc c Reemplazando 2 en 1:

4kgmg - T -keq = 0

6kgmg - keq - keq = 0 mg = 2 eq

grafica para el equilibrio:

OB De la figura:

eqyeq yeq/r = eq/2r eq = 2yeq..3

OB C

grafica cuando existe oscilacin:

eq usando la ecuacin de movimiento:

eqyeq Fy = m mg -T k (eq + A ) = m.

y luego: Mo = I = I = I/rA reemplazando y resolviendo en : Tr kr(eq + A ) = Multiplicando r a y resolviendo con Tr - kr(eq + A ) = 2r mgr - Tr - kr(eq + A) = mr mg 2kr eq 2kr A = 10r + 2r sabemos que A = 2y reemplazando: Reemplazando k en la ecuacin:

PROBLEMA 21-31. El bloque de 50 N de peso de la figura 21-31 se desliza por una superficie horizontal exenta de rozamiento mientras que el bloque de 25 N se mueve en un plano vertical. Los resortes estn sometidos a traccin en todo momento y las poleas son pequeas y exentas de rozamiento. Escribir la ecuacin diferencial del movimiento para la ecuacin x (t) del bloque de 50 N y determinar la frecuencia y el periodo de movimiento vibratorio resultante. 22

T= 2*3.1416/15.65T=0.40PROBLEMA 21-39.

SISTEMAS VIBRATORIOS VIBRACION LIBRE NO AMORTIGUADA