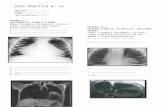
ALGEBRA LINEAL UNIDAD 1. NUMEROS COMPLEJOSUNIDAD 1 NUMEROS COMPLEJOS1.1 DEFINICIN Y ORIGEN DE LOS NMEROS COMPLEJOSLa primera referencia conocida a races cuadradas de nmeros negativos proviene del trabajo de los matemticos griegos, como Hern de Alejandra en el siglo I antes de Cristo, como resultado de una imposible seccin de una pirmide. Los complejos se hicieron ms patentes en el Siglo XVI, cuando la bsqueda de frmulas que dieran las races exactas de los polinomios de grados 2 y 3 fueron encontradas por matemticos italianos como Tartaglia, Cardano.Aunque slo estaban interesados en las races reales de este tipo de ecuaciones, se encontraban con la necesidad de lidiar con races de nmeros negativos. El trmino imaginario para estas cantidades fue acuado por Descartes en el Siglo XVII y est en desuso. La existencia de nmeros complejos no fue completamente aceptada hasta la ms abajo mencionada interpretacin geomtrica que fue descrita por Wessel en 1799, redescubierta algunos aos despus y popularizada por Gauss. La implementacin ms formal, con pares de nmeros reales fue dada en el Siglo XIX. Los algebristas de los siglos XV y XVI, al buscar una solucin para algunas ecuaciones de segundo grado, por ejemplo se encontraron con .Afirmaban que las ecuaciones no tenan solucin, ya que no hay ningn nmero real cuyo cuadrado sea un nmero negativo. Este hecho implicaba la conveniencia de "definir" nuevos nmeros de la forma: donde y son nmeros reales e es , que permitieran resolver cualquier ecuacin de segundo grado. Estos nuevos nmeros se llaman nmeros complejos ().Ejemplo:La ecuacin de segundo grado: tiene como solucin: Que expresaremos como: Se llama nmero complejo a toda expresin de la forma donde y son nmeros reales; i es la unidad llamada imaginaria, definida por las ecuaciones: o ; a es la parte real y b es la parte imaginaria del nmero complejo.Si a = 0, el nmero complejo 0 + b.i = b.i, es un nmero imaginario puro; si b = 0, se obtiene el nmero reala + 0.i = aDos nmeros complejos son iguales si: (a + b.i) = (c + d.i) a = c; b = d es decir, si son iguales sus partes reales e imaginarias por separado.Un nmero complejo es igual a cero si: a + b.i = 0 a = 0; b =0Ejercicios 1.11)

2)

Ya que

Por lo tanto

3)

Los angulos que forman 2 lados de un triangulo quilatero son de radianes, luego hay quie avanzar Por lo tanto, como uno de los 2 vertices es se tiene que

Son los otros dos. En forma binomica

1.2 OPERACIONES FUNDAMENTALES CON NMEROS COMPLEJOS. ADICCINDados los complejos Z1 = (a;b) y Z2 = (c ;d). Se define Z1 + Z2 = (a; b) + (c; d) = (a +c; b+ d)

SUSTRACCINSe obtiene sumando al minuendo el opuesto del sustraendo: Z1 + (-22) = (a; b) + (-c ; d) = (a c ; b-d)

MULTIPLICACINDados los complejos Z1 = (a ; b) y Z2 = (c ; d), se define Z1 * Z2 = (a*c-b*d; a*d + b*c)

POTENCIACINLa potenciacin de un numero complejo con potencia natural, se resuelve como una multiplicacin reiterada: Zn = (a ; b)n = (a ;b)1.(a ; b)2 (a ; b)n asociado de a dos pares los pares ordenados.

FORMA BINOMICALa forma Binomica de un numero complejo es: Z = a + bi

OPERACIONES DENMEROSCOMPLEJOS EN SU FORMA BINOMICA:La suma y diferencia de numeros complejos se realiza sumando y restando partes reales entre si y partesimaginariasentre si. +(a +bi) + (c + di) = (a+c) + (b+d) i -(a +bi) - (c + di) = (a-c) + (b-d) iMULTIPLICACIN CON NMEROS COMPLEJOSEl producto de los nmeros complejos se realiza aplicando la propiedaddistributivadel producto respecto de la suma y teniendo en cuenta que i2 = -1 (a + bi) (c + di) = (ac-bd) + (ad + bc) i

DIVISIN CON NMEROS COMPLEJOSEl cociente de nmeros complejos se hace racionalizando el denominador; esto es, multiplicando numerador y denominador por el conjugado de este.

Ejercicios:1)

2)

Agrupando los mismos trminos y aplicando la propiedad obtenemos,

3)

1.3 POTENCIAS DE I, MDULO O VALOR ABSOLUTO DE UN NMERO COMPLEJO.

POTENCIAS DE LA UNIDAD IMAGINARIA

Los valores se repiten de cuatro en cuatro, por eso, para saber cunto vale una determinada potencia de i, se divide el exponente entre 4, y el resto es el exponente de la potencia equivalente a la dada.

Ejemplo

VALOR ABSOLUTOEl valor absoluto, mdulo o magnitud de un nmero complejo z viene dado por la siguiente expresin: Si pensamos en z como un punto en el plano; podemos ver, por el teorema de Pitgoras, que el valor absoluto de un nmero complejo coincide con la distancia eucldea desde el origen del plano. Si el complejo est escrito en forma polar z = r ei, entonces |z| = r. Podemos comprobar con facilidad estas tres importantes propiedades del valor absoluto para cualquier complejo z y w. Por definicin, la funcin distancia queda como sigue d(z, w) = |z - w| y nos provee de un espacio mtrico con los complejos gracias al que se puede hablar de lmites y continuidad. La suma, la resta, la multiplicacin y la divisin de complejos son operaciones continuas. Si no se dice lo contrario, se asume que sta es la mtrica usada en los nmeros complejos.

Ejercicios 1.31)

2)

3)

Por propiedad del argumento

1.4 FORMA POLAR Y EXPONENCIAL DE UN NMERO COMPLEJO. FORMA POLAR

El producto de dos nmero complejos diferente de cero est dado en la forma polar por el producto de sus valores absolutos y la suma de sus argumentos. El cociente de dos nmeros complejos diferentes de cero est dado por el cociente de sus valores absolutos y la diferencia de sus argumentos.

ARGUMENTO DE UN NMERO COMPLEJO

El argumento de un nmero complejo es el ngulo que forma el vector con el eje real. Se designa por arg( z ).

FORMA EXPONENCIAL

A veces, y por simple comodidad se prefiere trabajar con la formatrigonomtricaen vez de con la forma binomica:Sea Z un nmero complejo cualquiera su representacin prdra experesarse de lassiguientesmaneras:

Forma Forma Forma Binomica trigonometrica exponencial

Donde

Y

Y

Ejercicios 1.4

1)

2)

3)

1.5 TEOREMA DE DE MOIVRE, POTENCIAS Y EXTRACCIN DE RACES DE UN NMERO COMPLEJO. TEOREMA DE DEMOIVRE Y POTENCIAS

Representacin polar de un nmero complejo

Donde la formula se usa cuando

En este casoy.==

En general, para cualquier otro prositivo k.

.

a esto se le conoce como Teorema de DeMoivre aplicable as mismo a las potencias de nmeros complejos

RACES DE UN NMERO COMPLEJO

Dado un nmero complejo que se define tal quei2=-1. Utilizando esta notacin podemos pensar en i como la raz cuadrada de 1, pero notamos que tambin tenemos(-i2)2=i2=-1, as que (i) es tambin una raz cuadrada de 1. Semejantemente a los nmeros reales, decimos que la raz cuadrada principal de 1 es i, o, en general, si x es cualquier nmero real positivo, entonces en la raz cuadrada principal de x se cumple la siguiente igualdad:

es decir, la raz cuadrada de un nmero negativo es necesariamente imaginario. Eso es debido a que , por lo que entonces:

Si se desea encontrar la raz de un nmero imaginario es posible demostrar laigualdad

Por los argumentos dados, i no puede ser ni positivo ni negativo. Esto crea un problema: para el nmero complejo z, no podemos definir para ser la raz cuadrada positiva de Z.

Para cada nmero complejo diferente a cero z existen exacto dos nmeros W tales quew2=Z . Por ejemplo, las races cuadradas de i son:

y..

La definicin general de est introduciendo el siguiente punto de rama: si z = rei es representado en coordenadas polares con < , despus fijamos el valor principal a:

As definido, la funcin de la raz es holomorfa en todas partes excepto en los nmeros reales no positivos, donde no es incluso continua. La antedicha serie de Taylor parasigue siendo vlida para el resto de los nmeros complejos xcon |x| < 1.

En general, para un nmero complejo expresado en forma rectangular, se obtiene:

Donde (el valor absoluto o mdulo del nmero complejo), y el signo de la parte imaginaria de la raz coincide con el signo de la parte imaginaria del radicando.

Ejercicios 1.5

Esta es la suma de los n primeros trminos de una progresin geomtrica de razn y primer trmino 1, es decir,

3)

Considerando ahora el producto

1.6 ECUACIONES POLINMICAS. Los nmeros complejos surgen ante la imposibilidad de hallar todas las soluciones de las ecuaciones polinmicas de tipo

Dados los valores apropiados de los coeficientes , esta ecuacin tendr n soluciones reales si que permitirn reescribir el polinomio de la siguiente forma:

Sin embargo, ecuaciones incluso tan sencillas como x2 + 1 = 0 desafan esta regla, ya que su solucin, que tericamente vendra dada por

que no existe en el campo de los reales ya que la raz cuadrada no est definida para argumentos negativos.

Los nmeros complejos sin embargo permiten ampliar an ms el concepto de "nmero", definiendo la unidad imaginaria o i como i =razde -1, lo que significara que la ecuacin anterior s tendra dos soluciones, que seran

La introduccin de los nmeros complejos permite probar el teorema fundamentaldel lgebra, que dice que cualquier ecuacin polinmica de grado n tieneexactamente n soluciones complejas.

De esta manera, se define genricamente un nmero complejo como un nmerocompuesto por dos partes, una parte real a y una parte imaginaria b,escribindose como sigue:

Por ejemplo,

Con los nmeros complejos se opera como se operara con productos de sumas ordinarios, teniendo en cuenta siempre que:

La divisin es un poco ms sofisticada debido a la necesidad de eliminar la unidad imaginaria del de nominador de la fraccin:

Ejercicios polinmicos:1.

2.

3.

Como

Se cumple que

Luego,

De donde,

De relacionar la tangente del angulo doble con la tangente se encontrara la rerlacion entre los coeficientes como

Entonces

La relacin buscada es

Ejercicios

2) Divisin

3) Raices

22