INTERPOLACION CON TRAZADORES O SPLINES

INTERPOLACION CON TRAZADORES O SPLINESY SU USO EN LA CORRECCION DE LOS RESULTADOS DE LOS ENSAYOS DE MECANICA DE SUELOS

00/00/2009UCVEnrique Coriat Celis

MTODOS PARA EL TRATO Y CORRECCIONES DE LAS CURVAS EN LOS ENSAYOS DE MECNICA DE SUELOS.INTERPOLACIN CON TRAZADORES O SPLINESDEFINICINEste tipo de interpolacin se llama Interpolacin Segmentara o interpolacin por splines. La idea central es que en vez de usar un solo polinomio para interpolar todos los datos, se pueden usar segmentos de polinomios entre pares coordenados de datos y unir cada uno de ellos adecuadamente para ajustar los datos. Una funcin spline esta formada por varios polinomios, cada uno definido en un intervalo y que se une entre si bajo ciertas condiciones de continuidad.Para un conjunto numeroso de puntos no es muy til calcular el polinomio interpolante que pasa por estos puntos, pues este tiende a tener grandes oscilaciones. Mas aconsejable es hacer una interpolacin secuencial de grado bajo sobre subconjuntos mas pequeos del total de puntos, definiendo as una funcin a trozos.FUNCIONES SPLINE DE GRADO 1Los splines de grado 1 son funciones polinomiales de grado 1 ( Rectas de la forma: f(x) = ax + b ) que se encargan de unir cada par de coordenadas mediante una recta.

Donde.

Donde.

Donde.

FUNCIONES SPLINE DE GRADO 2Los splines de grado 2 son funciones polinomiales de grado 2 ( De la forma: f(x) = ax + bx + c ) que se encargan de unir cada par de coordenadas mediante una curva.SPLINE DE GRADO 2( para cuatro puntos )Dado los datos:Un Spline cbico que interpola estos datos, es una funcin S( x ) definida de la siguiente manera:

( 1 )

( 2 )

( 3 )

( 4 )

( 5 )

( 6 )Para cada uno de los tres intervalos, se ha definido un par de funciones polinomiales de grado 2.Hasta aqu se tiene 6 ecuaciones vs 9 incgnitas. El siguiente paso es manejar la existencia de las derivadas continuas. En los puntos: 2 , 3 y 4 , 5.igualando ambas derivadas.

( 7 )

( 8 )De este modo se obtiene un total de 8 ecuaciones versus 9 incgnitas; esto da un grado de libertad para elegir alguna de las incgnitas. Se elige por simple conveniencia a1 = 0.Con lo que se hace un total de 8 ecuaciones con 8 incgnitas.

( 1 )

( 2 )

( 3 )

( 4 )

( 5 )

( 6 )

( 7 )

( 8 )Solucin Matricial

SPLINE DE GRADO 3 O SPLINE CUBICO Es el mtodo ms empleado debido a que proporciona un excelente ajuste a los puntos tabulados y su clculo no es excesivamente complejo.Est definido por un polinomio cbico de la forma. f (x) = ax + bx + cx + dSPLINE CUBICO ( Tres Puntos )Sean los puntosUn Spline cbico que interpola estos datos, es una funcin S( x ) definida de la siguiente manera:s1 ( x1 ) = y1a1x1 + b1x1 + c1x1 + d1 = y1 ( 1 )s1 ( x2 ) = y2a1x2 + b1x2 + c1x2 + d1 = y2( 2 )s2 ( x2 ) = y2a2x2 + b2x2 + c2x2 + d2 = y2 ( 3 )s2 ( x3 ) = y3a2x3 + b2x3 + c2x3 + d2 = y3( 4 )Hasta ac contamos con 4 ecuaciones y 8 incgnitas. Otra ecuacin se obtienen igualando la derivada de las ecuaciones ( 2 ) y ( 3 ) con lo que se asegura la continuidad en dicho punto; de la manera siguiente.3a1x22 + 2b1x2 + c1 = 3a2x22 + 2b2x2 + c23a1x22 + 2b1x2 + c1 - 3a2x22 - 2b2x2 - c2 = 0( 5 )Ahora contamos con 5 ecuaciones y 8 incgnitas. Otra ecuacin se obtienen igualando la segunda derivada de las ecuaciones ( 2 ) y ( 3 ) con lo que se asegura la continuidad en dicho punto; de la manera siguiente:6a1x2 + 2b1 = 6a2x2 + 2b26a1x2 + 2b1 - 3a2x22 - 2b2 = 0( 6 )Las dos ultimas ecuaciones se obtienen igualando a cero las segundas derivadas de las ecuaciones 1 , 4 con lo que se asegura que la doble derivada se anule en los puntos inicial y final.s1 ( x1 ) = 06a1x1 + 2b1 = 0 ( 7 )s2 ( x3 ) = 06a2x3 + 2b2 = 0( 8 )GENERALIZANDOa1x1 + b1x1 + c1x1 + d1 = y1 ( 1 )a1x2 + b1x2 + c1x2 + d1 = y2( 2 )a2x2 + b2x2 + c2x2 + d2 = y2 ( 3 )a2x3 + b2x3 + c2x3 + d2 = y3( 4 )3a1x22 + 2b1x2 + c1 - 3a2x22 - 2b2x2 - c2 = 0( 5 )6a1x2 + 2b1 - 3a2x22 - 2b2 = 0( 6 )6a1x1 + 2b1 = 0 ( 7 )6a2x3 + 2b2 = 0( 8 )Solucin Matricial

Ejemplo 1. Interpolar los siguientes datos mediante un spline cbicoSolucin: Se define el polinomio cbico en cada uno de los intervalos que se formanSi la curva grafica del spline cbico pasa por los puntos entonces debe cumplirse ques (x) = ys1 ( x ) = a1x + b1x + c1x + d1s1 ( 2 ) = - 1s ( 2 ) = 2a1 + 2b1 + 2c1 + d1 = - 1 s ( 2 ) = 8a1 + 4b1 + 2c1 + d1 = - 1 ( 1 )s1 ( 3 ) = 2s ( 3 ) = 3a1 + 3b1 + 3c1 + d1 = 2 s ( 3 ) = 27a1 + 9b1 + 3c1 + d1 = 2 ( 2 )s2 ( x ) = a2x + b2x + c2x + d2s2 ( 3 ) = 2s ( 3 ) = 3a2 + 3b2 + 3c2 + d2 = 2 s ( 3 ) = 27a2 + 9b2 + 3c2 + d2 = 2 ( 3 )s2 ( 5 ) = - 7s ( 5 ) = 5a2 + 5b2 + 5c2 + d2 = - 7 s ( 5 ) = 125a2 + 25b2 + 5c2 + d2 = - 7 ( 4 )Ahora se calcula la primera derivada de s1 ( x )s1 ( x ) = a1x + b1x + c1x + d1s ( x ) = 3a1x + 2b1x + c1Si x 2 , 3s ( x ) = 3a2x + 2b2x + c2Si x 3 , 53a1(3) + 2b1(3) + c1 = 3a2(3) + 2b2(3) + c227a1 + 6b1 + c1 = 27a2 + 6b2 + c2 ( 5 )De igual manera se calcula la segunda derivada.s ( x ) = 6a1x + 2b1Si x 2 , 3s ( x ) = 6a2x + 2b2Si x 3 , 56a1x + 2b1 = 6a2x + 2b26a1(3) + 2b1 = 6a2(3) + 2b218a1 + 2b1 = 18a2 + 2b2 ( 6 )En este punto contamos con 6 ecuaciones y 8 incgnitas, por lo tanto se tienen dos grados de libertad; en general, se agregan las siguientes dos condiciones:s ( xo ) = 0s ( xn ) = 0de lo cual se obtiene:Si s ( 2 ) = 06a1(2) + 2b1 = 012a1 + 2b1 = 0 ( 7 )s ( 5 ) = 06a2(5) + 2b2 = 030a2 + 2b2 = 0 ( 8 )

Con lo cual se ha completado un juego de 8 ecuaciones vs 8 incgnitas, como sigue

Luego:

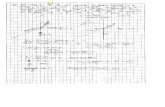
Observe la figura grafica conjunta de los dos polinomios cbicos que conforman el spline. No se nota que se trata de dos polinomios diferentes. Esto es debido a las condiciones que se pusieron sobre las derivadas de la funcin. Esta figura casi artstica, es la que permite aplicar los splines cbicos, para cuestiones como el diseo de letras por computadoras, o bien a problemas de aplicacin donde la interpolacin que se necesita es de carcter bastante delicado.SPLINE CUBICO( para cuatro puntos )Dado los datos:Un Spline cbico que interpola estos datos, es una funcin S( x ) definida de la siguiente manera:s1 ( x1 ) = y1a1x1 + b1x1 + c1x1 + d1 = y1 ( 1 )s1 ( x2 ) = y2a1x2 + b1x2 + c1x2 + d1 = y2( 2 )s2 ( x2 ) = y2a2x2 + b2x2 + c2x2 + d2 = y2 ( 3 )s2 ( x3 ) = y3a2x3 + b2x3 + c2x3 + d2 = y3( 4 )s3 ( x3 ) = y3a3x3 + b3x3 + c3x3 + d3 = y3 ( 5 )s3 ( x4 ) = y4a3x4 + b3x4 + c3x4 + d3 = y4( 6 )Hasta ac contamos con 6 ecuaciones y 12 incgnitas. Otras dos se obtienen igualando la derivada de las ecuaciones ( 2 ) , ( 3 ) y ( 4 ) y ( 5 ) con lo que se asegura la continuidad en dichos puntos; de la manera siguiente.3a1x22 + 2b1x2 + c1 = 3a2x22 + 2b2x2 + c23a1x22 + 2b1x2 + c1 - 3a2x22 - 2b2x2 - c2 = 0( 7 )3a2x32 + 2b2x3 + c2 = 3a3x32 + 2b3x3 + c33a2x32 + 2b2x3 + c2 - 3a3x32 - 2b3x3 - c3 = 0( 8 )Ahora contamos con 8 ecuaciones y 12 incgnitas. Otras dos se obtienen igualando la segunda derivada de las ecuaciones ( 2 ) , ( 3 ) y ( 4 ) y ( 5 ) con lo que se asegura la continuidad en dichos puntos; de la manera siguiente:6a1x2 + 2b1 = 6a2x2 + 2b26a1x2 + 2b1 - 6a2x2 - 2b2 = 0( 9 )6a2x3 + 2b2 = 3a3x3 + 2b36a2x3 + 2b2 - 6a3x2 - 2b3 = 0( 10 )Las dos ultimas ecuaciones se obtienen igualando a cero las segundas derivadas de las ecuaciones 1 , 6 con lo que se asegura que la doble derivada se anule en los puntos inicial y final.s1 ( x1 ) = 06a1x1 + 2b1 = 0 ( 11 )s3 ( x4 ) = 06a3x4 + 2b3 = 0( 12 )Generalizando:a1x1 + b1x1 + c1x1 + d1 = y1 ( 1 )a1x2 + b1x2 + c1x2 + d1 = y2( 2 )a2x2 + b2x2 + c2x2 + d2 = y2 ( 3 )a2x3 + b2x3 + c2x3 + d2 = y3( 4 )a3x3 + b3x3 + c3x3 + d3 = y3 ( 5 )a3x4 + b3x4 + c3x4 + d3 = y4( 6 )3a1x22 + 2b1x2 + c1 - 3a2x22 - 2b2x2 - c2 = 0( 7 )3a2x32 + 2b2x3 + c2 - 3a3x32 - 2b3x3 - c3 = 0( 8 )6a1x2 + 2b1 - 6a2x2 - 2b2 = 0( 9 )6a2x3 + 2b2 - 6a3x2 - 2b3 = 0( 10 )6a1x1 + 2b1 = 0 ( 11 )6a3x4 + 2b3 = 0( 12 )Solucin Matricial

Ejemplo 4: interpolar los siguientes datos utilizando spline cbico

Solucin: Definicin del polinomio cbico en cada uno de los intervaloss ( x ) = a1x + b1x + c1x + d1 Si:x - 1 , 1s ( x ) = a2x + b2x + c2x + d2 Si:x 1 , 2s ( x ) = a3x + b3x + c3x + d3 Si:x 2 , 4

Para que los splines pase por los puntos del intervalo debe cumplirse que:s ( -1 ) = -1a1(-1) + b1(-1) + c1(-1) + d1 = -1- a1 + b1 - c1 + d1 = -1( 1 )s ( 1 ) = 1a1(1) + b1(1) + c1(1) + d1 = -1 a1 + b1 + c1 + d1 = 1( 2 )a2(1) + b2(1) + c2(1) + d2 = -1 a2 + b2 + c2 + d2 = 1( 3 )s ( 2 ) = 5a2(2) + b2(2) + c2(2) + d1 = 5 8a1 + 4b1 + 2c1 + d1 = 5( 4 )a3(2) + b3(2) + c3(2) + d3 = 5 8a3 + 4b3 + 2c3 + d3 = 1( 5 )s ( 4 ) = -2a3(4) + b3(4) + c3(4) + d4 = -264a3 + 16b3 + 4c3 + d3 = -2( 6 )Calculo de la primera derivada:s ( x ) = a1x + b1x + c1x + d1 s ( x ) = 3a1x + 2b1x + c1s ( x ) = a2x + b2x + c2x + d2 s ( x ) = 3a2x + 2b2x + c2s ( x ) = a3x + b3x + c3x + d3 s ( x ) = 3a3x + 2b3x + c3

Las posibles discontinuidades de s(x) son x = 1 y x = 2. Por lo tanto para hacer que s(x) sea continua, se igualen las ecuaciones correspondientes en ambos valores.* 3a1x + 2b1x + c1 = 3a2x + 2b2x + c2 3a1(1) + 2b1(1) + c1 = 3a2(1) + 2b2(1) + c2 3a1 + 2b1 + c1 = 3a2 + 2b2 + c2* 3a2x + 2b2x + c2 = 3a3x + 2b3x + c3 3a2(2) + 2b2(2) + c2 = 3a3(2) + 2b3(2) + c3 12a2 + 4b2 + c2 = 12a3 + 4b3 + c3Calculo de la segunda derivadas ( x ) = 3a1x + 2b1x + c1s ( x ) = 6a1x + 2b1s ( x ) = 3a2x + 2b2x + c2s ( x ) = 6a2x + 2b2s ( x ) = 3a3x + 2b3x + c3s ( x ) = 6a3x + 2b3De igual manera las posibles discontinuidades son x = 1 y x = 2. por lo tanto, para que s(x) sea continua, se igualan las ecuaciones en ambos valores:6a1x + 2b1 = 6a2x + 2b2 3a1x + b1 = 3a2x + b2 12a2x + 2b2 = 12a3x + 2b3 6a2x + b2 = 6a3x + b3 Finalmente se agregan las condiciones de que la doble derivada se anule en los puntos inicial y final de la tabla. En este caso:s ( -1 ) = 0s ( x ) = 6a1x + 2b1- 3a1 + 2b1 = 0s ( 4 ) = 0s ( x ) = 6a3x + 2b312a3 + b3 = 0con esto se han formado un sistemas de ecuaciones lineales con 12 ecuaciones y 12 variables. - a1 + b1 - c1 + d1 = -1a1 + b1 + c1 + d1 = 1a2 + b2 + c2 + d2 = 18a2 + 4b2 + 2c2 + d2 = 58a3 + 4b3 + 2c3 + d3 = 564a3 + 16b3 + 4c3 + d3 = - 23a1 + 2b1 + c1 = 3a2 + 2b2 + c212a2 + 4b2 + c2 = 12a3 + 4b3 + c33a1 + b1 = 3a2 + b26a2 + b2 = 6a3 + b3- 3a1 + 2b1 = 012a3 + b3 = 0

Solucin del sistema mtodo matricial.

a1 -11-1100000000-1b1 1111000000001c1 0000111100001d1 0000842100005a2 0000000084215b2 00000000641641-2c2 3210-3-2-1000000d2 000012410-12-4-100a3 3100-3-10000000b3 00006100-6-1000c3 -3100000000000d3 00000000121000a1 0.043-0.043-0.1000.1000.007-0.0070.086-0.0140.052-0.019-0.2240.010-1b1 0.129-0.129-0.3000.3000.021-0.0210.257-0.0430.157-0.0570.3290.0291c1 -0.5430.5430.100-0.100-0.0070.007-0.0860.014-0.0520.0190.224-0.0101d1 0.3710.6290.300-0.300-0.0210.021-0.2570.043-0.1570.057-0.329-0.0295a2 -0.1000.1000.400-0.400-0.1000.100-0.2000.2000.2670.2670.133-0.1335b2 0.557-0.557-1.8001.8000.343-0.3431.114-0.686-1.486-0.914-0.7430.457-2c2 -0.9710.9711.600-1.600-0.3290.329-1.9430.6572.5900.8761.295-0.4380d2 0.514-0.5140.8000.2000.086-0.0861.029-0.171-1.371-0.229-0.6860.1140a3 0.007-0.007-0.1000.1000.043-0.0430.014-0.086-0.0190.052-0.0100.2240b3 -0.0860.0861.200-1.200-0.5140.514-0.1711.0290.229-0.6290.114-1.6860c3 0.314-0.314-4.4004.4001.386-1.3860.629-3.771-0.8382.305-0.4193.8480d3 -0.3430.3434.800-4.800-0.0571.057-0.6864.1140.914-2.5140.457-2.7430a1 0.3643Luego las funciones son:b1 1.0929c1 0.6357 s ( x ) = 0.3643x + 1.0929x + 0.6357x - 1.093d1 -1.0929a2 -2.1 s( x ) = - 2.1x + 8.4857x - 6.757x + 1.3714b2 8.4857c2 -6.7571 s ( x ) = 0.6857x - 8.229x + 26.671x - 20.91d2 1.3714a3 0.6857b3 -8.2286c3 26.671d3 -20.914

Grafica:

REGLA PARA ENCONTRAR MXIMOS Y MNIMOS

Si la funcin f (x) est definida en el intervalo a < x < b , tiene una derivada , y esta es cero en el punto x = c, y si < 0 en el punto x = c , entonces f (x) tiene un mximo en el punto ( c , f (c) ). Si C > 0 en el punto x = c y = 0 en el mismo punto, entonces f (x) tiene un mnimo en el ( c , f (c) ) y Si = 0 en el punto x = c entonces no se puede afirmar si hay un mximo y un mnimo en el punto x = c.Ejemplo: Establecer los mximos y mnimos de la funcin: f ( x ) = x - 3x + 13Solucin: si: f ( x ) = x - 3x + 13f (x) = 3x - 6x

= 03x - 6x = 0x = 0 , x = 2

= 6x - 6 = 6 (0) 6 = -6* Hay un mximo en el punto ( 0 , f (0) )( 0 , 13 )

= 6x - 6 = 6 (2) 6 = 6* Hay un mnimo en el punto ( 2 , f (2) )( 0 , 9 )

APROXIMACIN CON MNIMOS CUADRADOS (Anlisis de Regresin)

Los mtodos de aproximacin funcional exacta estudiados hasta ac nos han permitido establecer una funcin de aproximacin al ser tabulado que contenga a los puntos dados. Sin embargo, a veces la informacin dada en la tabla tiene errores significativos; por ejemplo cuando provienen de medidas fsicas; en estas circunstancias no tiene sentido establecer una funcin de aproximacin por los puntos dados, sino solo cerca de ellos. No obstante, esto crea un problema, ya que se pueden obtener un nmero infinito de curvas entre los puntos. Para determinar la mejor curva se establece un criterio que la fije y una metodologa que lo determine. El criterio es pedir que la suma de las distancias calculadas entre el valor de la funcin que aproxima P(xi) y el valor de la funcin f(xi) dada en la tabla, sea mnima.

Es decir. Para evitar problemas de derivalidad mas adelante, se acostumbra utilizar las distancias di elevadas al cuadrado.

si se utiliza P(x) = ao + a1x para aproximar la funcin dada, el problema queda como el de minimizar.

Ntese que del nmero infinitos de polinomios que pasen entre los puntos, se selecciona aquellos cuyos coeficientes ao y a1 minimicen la anterior.En el clculo de funciones de una variable, establece que para encontrar el mnimo o mximo de una funcin, se deriva y se iguala con cero esa derivada. Despus se resuelve la ecuacin resultante para obtener los valores de la variable que pudieran minimizar o maximizar la funcin. En el caso en estudio, donde se tiene una funcin por minimizar de dos variables ( ao y a1 ), el procedimiento es derivar parcialmente con respecto a cada una de las variables e igualar a cero cada derivada, con lo que se obtienen dos ecuaciones algebraicas en las incgnitas ao y a1 ; o sea

se deriva dentro del signo de sumatoria

Desarrollada y simplificadas quedan

Resuelto el sistema mediante la regla de cramer se obtiene

Donde

Mtodo Matricial:

Resolviendo mediante el mtodo matricialLa funcin P(x) = ao + a1x es la aproximacin de primer grado que mejor ajusta la informacin tabulada. Este polinomio puede usarse a fin de aproximar valores de la funcin para argumentos no conocidos en la tabla.Regresin no LinealLa regresin lineal proporciona una poderosa tcnica para ajustar la mejor lnea a los datos histricos. Sin embargo el modelo se basa en el hecho de que las variables dependiente e independiente mantienen una relacin lineal. Lo cual no siempre ocurre, en ocasiones el comportamiento de las variables es exponencial,. Estos datos pueden ser linealizados transformndolos logaritmicamente antes de efectuar el modelo de regresin lineal, a este proceso se conoce como Regresin no lineal.Pronsticos mediante ajustes polinomialesEl grado de la funcin no tiene relacin con el nmero de puntos usados y debe relacionarse de antemano con base en consideraciones tericas que apoyan el fenmeno estudiado.El hecho de tener la mejor recta que aproxime la informacin, no significa que la informacin este bien aproximada; quiz convenga aproximarla con una parbola o una cbica.Para encontrar la funcin de segundo grado P2(x) = ao + a1x + a2x que mejor aproxime los datos tabulados.

Resolviendo el sistema (mtodo matricial)

Para encontrar la funcin de tercer grado P3(x) = ao + a1x + a2x + a3x3 que mejor aproxime los datos tabulados.

Resolviendo el sistema.

Generalizando:

Resolviendo el sistema de forma general

En el proceso de construccin de modelos matemticos a partir de datos histricos Pronsticos la graficacin o de los datos en un Sistema Coordenado Cartesiano permite tener informacin visual del comportamiento del fenmeno en estudio, as por ejemplo:Si los puntos correspondientes a los datos, estn dispersos en torno a una recta, entonces lo mas aconsejable es el modelo lineal de mnimos cuadrados.Si los puntos correspondientes a los datos, estn dispersos en torno a una parbola, entonces lo mas aconsejable es el modelo polinomial de segundo grado. Y as sucesivamente. Dada una funcin y = f(x) en forma tabular, a menudo se desea encontrar el valor de x correspondiente a un valor dado de y, este proceso llamado interpolacin inversa, constituye el soporte matemtico en pronsticos. Cuando los datos son extrados de un proceso ya ocurrido y cuidadosamente observado, se llaman datos histrico

Aproximacin Matrilineal con Mnimos CuadradosCon frecuencia se tienen funciones de mas de una variable; esto es f(u , v , z). si se sospecha una funcionalidad lineal en las distintas variables; es decir, si se piensa que la funcin y = ao + a1u + a2v + a3z puede ajustar los datos de la siguiente tabla.

PuntosUVZy

1u1v1Z1f ( u1 , v1 , z1 )

2u2v2Z2f ( u2 , v2 , z2 )

3u3v3Z3f ( u3 , v3 , z3 )

.....

Mumvmzmf ( um , vm , zm )

Se puede aplicar el mtodo de los mnimos cuadrados para determinar los coeficientesao , a1 , a2 y a3 que mejor aproximen la funcin de varias variables tabulada.el procedimiento es anlogo al descrito anteriormente y consiste en minimizar la funcin.

Que de derivada parcialmente con respecto de cada coeficiente por determinar: ao , a1 , a2 y a3 e igualada a cero cada una, queda.

Ecuaciones que arregladas generan el sistema algebraico lineal siguiente:

Donde:

Para una funcin de dos variable u , v se tiene: