MÓDULO V SISTEMA DE ECUACIONES FUNCIONES · 2019. 8. 22. · Solución :{(4:2)} Método de...

ANEXO CIU 2019

DEPARTAMENTO DE ECONOMÍA PRODUCCIÓN E INNOVACIONES

TECNOLÓGICAS:

LICENCIATURA EN ADMINISTRACIÓN DE EMPRESAS

TECNICATURA EN ANALISTA PROGRAMADOR UNIVERSITARIO

MÓDULO V

SISTEMA DE

ECUACIONES

FUNCIONES

Universidad Nacional de José C. Paz Secretaría Académica Dirección General de Acceso y Apoyo al Estudiante Equipo de Coordinación y Asesores de Matemática Ciclo de Inicio Universitario

1

Ecuación de primer grado o lineal con dos incógnitas:

2x + 4y = 8

Coeficiente de y

Retomando un poco!!!

Ya vimos en el anexo III de Ecuaciones, que una ecuación en una variable (𝒙), llamada incógnita, es una igualdad entre dos expresiones algebraicas que contienen a dicha variable. Las ecuaciones frecuentemente surgen de expresar en lenguaje algebraico una situación problemática planteada en lenguaje coloquial. Una vez interpretada la situación problema en un lenguaje propio de la matemática es posible trabajar con dicha expresión para llegar a la solución buscada.

Hemos dicho también, que cada valor de la variable (𝒙) para el que se verifica o satisface la ecuación, se la denomina solución de la ecuación. El conjunto de todas las soluciones se la denomina conjunto solución de la ecuación. Si la incógnita se encuentra elevada a un exponente 1, la ecuación es lineal o de primer grado. Una ecuación lineal con una incógnita puede tener ninguna, una o más de una solución.

Cuando ningún valor de la variable (𝒙) satisface a la ecuación, diremos que el conjunto solución es vacío y lo simbolizamos: S = Ø o bien S = {}.

Observemos la siguiente expresión: 2𝑥 + 4𝑦 = 8, es un ejemplo de una ecuación lineal

de dos variables. Para resolverla debemos averiguar los valores de “𝑥” e “𝑦” que verifican la igualdad. Dentro de las soluciones que podemos encontrar se hayan todos los pares de la forma (𝑥; 𝑦):

(2; 1); (-1; 5

2); (0; 2); (6; -1); (0,5; 1,75); (

7

2 ;

1

4); etc….

Todos estos pares de valores verifican simultáneamente la ecuación, ya que la suma da por resultado 8. Pero además de estos pares de valores existen otros infinitos pares que verifican la ecuación, por lo que podemos decir que existen infinitas soluciones para este tipo de ecuaciones. Cada una de ellas puede ser interpretada como un punto de coordenadas (x; y) sobre la recta cuya ecuación es 2x + 4y = 8 Para encontrar los pares de valores que pertenecen a una recta y que verifican su

ecuación, se despeja una de las variables, en nuestro caso: y = −1

2 𝑥 + 2

A continuación te mostramos el gráfico correspondiente a y = −1

2 𝑥 + 2, con los pares de

puntos (𝑥; 𝑦) señalados arriba:

Coeficiente de y

Término independiente


2

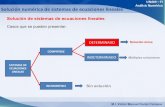
Sistema de dos ecuaciones lineales con dos incógnitas

Un sistema de dos ecuaciones lineales con dos incógnitas está formado por dos ecuaciones lineales de las que se busca una solución común. Resolver un sistema de dos ecuaciones lineales con dos incógnitas significa hallar, si es que existen, todos los pares (𝑥 ; 𝑦) que satisfacen ambas ecuaciones simultáneamente. Para hallar la solución de un sistema de dos ecuaciones lineales con dos incógnitas, se puede aplicar distintos métodos. En este repaso veremos algunos de ellos.

Método de Igualación:

4𝑥 + 3𝑦 = 22

2𝑥 + 5𝑦 = 18

1º- Despejamos una de las dos variables (x o y) en las dos ecuaciones. Elegimos despegar la “y”

4𝑥 + 3𝑦 = 22 2𝑥 + 5𝑦 = 18

3𝑦 = 22 – 4𝑥 5𝑦 = 18 – 2𝑥

A - 𝑦 = 22−4𝑥

3 B- 𝑦 =

18−2𝑥

5

2º- Como los primeros miembros de cada ecuación despejada son iguales(A y B), entonces, los

segundos también lo son. En consecuencia, igualamos (de ahí, el nombre del método):

22−4𝑥

3=

18−2𝑥

5

3º- Partimos de un sistema de dos ecuaciones con dos incógnitas y llegamos a una ecuación con

una incógnita. Para resolverla, aplicamos la propiedad fundamental de las proporciones y la propiedad

distributiva de un producto respecto de una suma o resta:

5. (22 – 4𝑥) = 3. (18 – 2𝑥)

110 − 20𝑥 = 54 – 6𝑥

−20𝑥 + 6𝑥 = 54 – 110


3

− 14𝑥 = −56

𝑥 = − 56: (−14) => 𝑥 = 4

4º - El valor obtenido se reemplaza en cualquiera de las expresiones A o B en que aparece

despejada la otra incógnita.

Vamos a reemplazarlo en las dos para comprobar que en ambos casos debe darnos el mismo

valor de la otra incógnita.

Si elegimos A tenemos: 𝑦 =22−4.4

3 => 𝑦 =

22−16

3 => 𝑦 =

6

3 => 𝑦 = 2

Si elegimos B tenemos: 𝑦 =18−2.4

5 => 𝑦 =

18−8

5 => 𝑦 =

10

5 => 𝑦 = 2

La solución del sistema es S:{(4;2)}

Verificación:

4. 𝑥 + 3. 𝑦 = 22 2. 𝑥 + 5. 𝑦 = 18

4. 4 + 3. 2 = 22 2. 4 + 5. 2 = 18

16 + 6 = 22 8 + 10 = 18

22 = 22 18 = 18

Veamos cuál es el procedimiento si se resuelve este sistema de dos ecuaciones lineales

con dos incógnitas por otro método.

Método de Sustitución:

4𝑥 + 3𝑦 = 22

2𝑥 + 5𝑦 = 18

1º- Despejamos una de las dos variables ( 𝑥 o 𝑦) en una de las ecuaciones. Elegimos la primera

ecuación y de ella despegamos la “𝑦”

4𝑥 + 3𝑦 = 22

𝑦 = 22−4𝑥

3

2º- Reemplazamos la variable por expresión hallada en la otra ecuación

2𝑥 + 5𝑦 = 18

2𝑥 + 5. (22−4𝑥

3) = 18

2𝑥 +110

3 -

20

3𝑥 = 18

2𝑥 − 20

3𝑥 = 18 −

110

3

−14𝑥 = −56

3

𝑥 = −56

3: (−

14

3)

𝑥 = 4


4

Luego reemplazamos el valor de “𝑥” obtenido, en la ecuación despejada para obtener el

valor

de “𝑦”. En nuestro ejemplo: 𝑦 = 22−4𝑥

3 => 𝑦 = (22 – 4.4): 3 => 𝑦 = 2

Solución :{(4:2)}

Método de reducción por sumas y restas Consiste en lograr que una de las variables llegue a tener el mismo coeficiente en las dos ecuaciones, ya que de esta manera, al restar miembro a miembro ambas ecuaciones, se elimina dicha incógnita. Si esto sucede, trabajaremos con una ecuación y una sola incógnita (la que no se eliminó), que al resolverla obtenemos su valor y reemplazando en cualquiera de las ecuaciones primitivas, se obtiene el valor de la otra incógnita. Veamos el ejemplo:

4𝑥 + 3𝑦 = 22

2𝑥 + 5𝑦 = 18

Multiplicamos la segunda ecuación por 2, restamos y resulta:

4𝑥 + 3𝑦 = 22

4𝑥 + 10𝑦 = 36

−7𝑦 = −14 => 𝑦 = −14: (−7) => 𝒚 = 𝟐 Elegimos la primera o segunda ecuación y calculamos el valor de x

4𝑥 + 3𝑦 = 22 => 4𝑥 + 3. (2) = 22 => 4𝑥 = 22 – 6 => 𝑥 = 16: 4 => 𝒙 = 𝟒

Solución :{(4:2)}

Método de determinantes Hasta el momento hemos buscado la solución de sistemas de dos ecuaciones con dos

incógnitas (2x2) por medio de los métodos de igualación, sustitución y reducción, que nos

han mostrado que la resolución por estos procedimientos, nos llevan a la misma solución

del sistema. Ahora te presentaremos otra forma de realizar la solución de los mismos

sistemas de ecuaciones por medio de una regla llamada Regla de Cramer a partir de

determinantes.

La regla de Cramer es un método para resolver, mediante el uso de determinantes, sistema

de ecuaciones cuadrados, es decir, que contengan el mismo número de ecuaciones que de

incógnitas.

El procedimiento lo explicamos para un sistema de dos ecuaciones con dos incógnitas y se

puede extender para cualquier sistema de n ecuaciones con n incógnitas(n x n).

Sea por ejemplo el sistema de 2x2:

a1x + b1y = c1 donde, a1, b1, c1, a2, b2 y c2 son números reales

a2x + b2y = c2

a1, b1, a2, b2 son los coeficientes de las incógnitas, mientras que c1 y c2 son los términos

independientes.


5

Para resolver este sistema y cualquier otro, debes en primer lugar, asegurarte que las

ecuaciones estén expresadas de la forma a.x + b.y = c, de lo contrario, realizaras los

pasajes necesarios para que lo estén. Luego debes hallar tres determinantes que

denotaremos: ∆( determinante general); ∆x (determinante en x) y ∆y (determinante en y)

El determinante general tiene filas y columnas conformadas por los coeficientes de las

Incógnitas.

∆ = |𝑎1 𝑏1

𝑎2 𝑏2|

En la fila uno del determinante, tenemos los coeficientes de x e y correspondientes a la

primera ecuación y en la fila dos los coeficientes de “x” e “y” correspondientes a la

segunda ecuación. En cuanto a columnas se refiere, en la primera, tenemos los

coeficientes de “x” de la primera y segunda ecuación y en la segunda columna, tenemos

los coeficientes de “y” correspondientes a la primera y segunda ecuación.

La diagonal principal del determinante esta formada por a1 y b2, la diagonal secundaria la

forman a2 y b1.

Para resolver el determinante, Siempre restamos el producto de la diagonal principal

menos el producto de la diagonal secundaria, resultando: ∆ = a1.b2 – a2.b1

Para calcular los determinantes específicos (∆x, ∆y), reemplazamos por los términos

independientes la columna correspondiente a los coeficientes de dichas variables

∆x = |𝑐1 𝑏1

𝑐2 𝑏2| ∆y = |

𝑎1 𝑐1

𝑎2 𝑐2|

Nos queda el último paso, que es calcular el valor de cada variable. Para hallarlas,

realizamos la siguiente operación:

x = ∆𝒙

∆ y =

∆𝒚

∆

Veamos el ejemplo propuesto al inicio, con el que aplicamos los otros métodos

4x + 3y = 22 2x + 5y = 18

1º- Calculamos el determinante general △

△= |4 32 5

| => △ = 4.5 – 2.3 => △ = 14


6

2º - Calculamos los determinantes específicos de cada variable

△ 𝒙 = |22 318 5

| => △ 𝒙 = 22.5 – 18.3 = 56

△ 𝒚 = |4 222 18

| => △y = 4.18 – 2.22 = 28

3º - Para encontrar el valor de cada variable, procedemos a realizar las divisiones

siguientes: 𝑥 = △𝑥

△ 𝑦 =

△𝑦

△

En nuestro ejemplo:

𝑥 = 56

14 => 𝑥 = 4 𝑦 =

28

14 => 𝑦 = 2

Solución: {(4; 2)}

Método Gráfico Para encontrar la solución a un sistema de dos ecuaciones con dos incógnitas a través del método gráfico, necesitamos que cada ecuación se exprese de la forma: y = m. x + b.

( m ∈ ℝ y b∈ ℝ) Por lo dicho anteriormente, en cada ecuación debemos despejar la variable “y”.

Volviendo a la expresión y = m. x + b, m es la pendiente y nos indica la inclinación (𝜶), respecto del eje x, que tiene la recta que representa a dicha ecuación. El término b es la ordenada al origen, el punto donde la recta corta al eje “y” o eje de ordenadas.

m = tg𝛼 = tg𝛽 = 𝑦1

𝑥1

b: ordenada al origen

r: intersección de la recta con el eje x

ᾳ: ángulo que forma la recta con el eje x

ᾳ = β: ángulos correspondientes entre paralelas

Se utilizan varios métodos para representar funciones: tablas de valores, intersecciones con ambos ejes, representar por el método de pendiente y ordenada al origen, etc En esta oportunidad te recordaremos el método de pendiente y ordenada al origen

Para ello seguimos los siguientes pasos:

1º- Marcamos sobre el eje “y” la ordenada al origen(b). Si ésta es fracción, hacemos el

pasaje correspondiente a decimal para ubicarla con facilidad. Obtenemos así el primer

punto (1).


7

2º- Tomamos la pendiente (m). Conviene que este expresada en fracción (𝑚 = 𝑎

𝑐 ). Si el

número es entero, lo expresamos como fracción de denominador 1. Si el número es

decimal, buscamos su expresión en fracción correspondiente.

El denominador de la fracción nos indica cuantas unidades, a partir del punto anterior

(1), nos debemos desplazar a la derecha. Al realizar este movimiento, obtenemos el

segundo punto (2).

El numerador de la fracción nos indica cuantas unidades, a partir del punto anterior

(2), debemos subir (si la fracción es positiva) o bajar (si la fracción es negativa),

obteniendo de esta manera el tercer punto (3).

3º- Unimos el primer punto con el último y nos queda determinada la recta que

representa a la función lineal correspondiente.

Veamos nuestro ejemplo:

4x + 3y = 22 2x + 5y = 18 Despejamos en ambas ecuaciones la variable “y”

A - 𝑦 = 22−4𝑥

3 B- 𝑦 =

18−2𝑥

5

Ordenamos los términos en cada expresión, llevándolos a la forma: y = mx + b

𝑦 = −4

3𝑥 +

22

3 𝑦 = −

2

5𝑥 +

18

5

Es conveniente, para comenzar con la gráfica de cada función, hacer el pasaje de la

ordenada al origen a su expresión decimal, para ubicarla en el eje “y”.

22

3= 7. 3̅

18

5= 3,6


8

Clasificación de los sistemas según la solución

En un sistema de ecuaciones lineales con dos incógnitas, cada ecuación representa una recta en el plano. Discutir un sistema es estudiar la situación de estas rectas en el plano, que pueden ser:

a- Compatible determinado. El sistema admite solución y es única. Las rectas que representan a cada ecuación son Secantes (se cortan en un punto).

b- Compatible indeterminado. El sistema admite infinitas soluciones. Las rectas que representan a cada ecuación son paralelas coincidentes (se cortan en todos sus puntos).

c- Sistema Incompatible. El sistema no tiene solución. Las rectas que representan a cada ecuación resultan paralelas (no se cortan en ningún punto).

En la figura A podemos observar representado el sistema: 2x + y = 4 x + 3y = 7 Es compatible determinado, admite una única solución y por lo tanto las rectas que representan a cada ecuación se cortan en ese punto (1; 2).


9

En la figura B, te mostramos la representación de un sistema que admite infinitas soluciones, ya que las rectas que corresponden a cada ecuación son coincidentes, por lo tanto tienen todos sus puntos en común. El sistema que se represento es el siguiente: -2x + y = -4 6x – 3y = 12

En la figura C se representó un sistema Incompatible, es decir, que no tiene solución. Las rectas que representan a cada ecuación son paralelas, por lo tanto no tienen ningún punto en común. El sistema representado fue el siguiente:

-4x +y = 3 -4x +y = -1 ¿Cómo nos damos cuenta que un sistema es compatible (determinado o indeterminado) o incompatible si no lo representamos? Tomamos los ejemplos de la figura B y C, para que puedas observar que sucede cuando

resuelves por algún método de los que explicamos, un sistema que no tiene solución o la

tiene, pero son infinitas. Ya hemos resuelto sistemas en donde si la tienen.

Si el sistema no tiene solución y el método que aplicamos es el de Determinantes, sucede


10

lo siguiente:

-4x +y = 3 △= |−4 1−4 1

| => △ = -4.1 – (-4).1 => △ = -4 + 4 => △ = 0

-4x +y = -1

△ 𝒙 = |3 1−1 1

| => △ 𝒙 = 3.1 – (-1).1 = 4 △ 𝒚 = |−4 3

−4 − 1| => △y = -4. (-1) – (-4). 3 = 16

𝑥 = △𝑥

△=> 𝑥 =

4

0 𝑦 =

△𝑦

△=> 𝑦 =

16

0 No podemos dividir por cero!!!!!

Cuando el determinante general nos da cero y los de cada variable son distintos de cero,

el sistema no tiene solución, por lo tanto es Incompatible.

Veamos el sistema de la figura B

-2x + y = -4 △= | −2 1 6 − 3

| => △ = -2. (-3) – 6.1 => △ = 6 - 6 => △ = 0

6x – 3y = 12

△ 𝒙 = |−4 1

12 − 3| => △ 𝒙 = -4. (-3) – 12.1 =>△ 𝒙 = 12 – 12 => △ 𝒙 = 0

△ 𝒚 = |−2 − 4 6 12

| => △y = -2.12 – 6. (-4) =>△y = -24 + 24 => △y =0

𝑥 = △𝑥

△=> 𝑥 =

0

0 𝑦 =

△𝑦

△=> 𝑦 =

0

0

Cuando el determinante general y los de cada variable nos dan cero, el sistema admite

infinitas solución, por lo tanto, es Compatible indeterminado.

Sistemas equivalentes: Dos sistemas son equivalentes si tienen el mismo conjunto

solución.

Si en un sistema de ecuaciones se permutan dos ecuaciones, se obtiene un sistema

equivalente.

Si una ecuación de un sistema se multiplica por un número real distinto de cero, se

obtiene un sistema equivalente al primero.

Si una ecuación de un sistema se sustituye por la suma de ella con otra multiplicada por

un número real distinto de cero, se obtiene un sistema equivalente al primero

Actividad Nº1

Intenta resolver los sistemas de la figura B y C, aplicando cualquiera de los otros Métodos (sustitución, igualación y reducción por sumas y restas)

Actividad Nº2

Representa las siguientes funciones, indicando ordenada y pendiente en cada caso.

a) f(x) = 3

5 x – 6 b) g(x) = -

5

4 x + 3 c) h(x) = 2x -

1

2 d) r(x) = -0.5x +1

e) s(x) = 5

−2 x -

8

5 f) t(x) = -5 g) u(x) = 4,5x


11

Actividad Nº 3

La ordenada al origen b y la pendiente m de la recta cuya ecuación es 𝑥

2 +

𝑦

3 = 1 son

respectivamente:

a) b = 1 y m = 2

3 c) b = 1 y m = -

3

2

b) b = 1 y m = - 2

3 d) b = 3 y m = -

3

2

Actividad Nº4 Indique la pendiente y la ordenada al origen en cada caso:

a) 3x + y = 5 b) 2x – 3y = 6 c) -2y = x

d) y = 𝑥+𝑦

2 e) 4x + 2y – 7 = 0 f) 4 – y = 0

Actividad Nº5

Resuelve los siguientes sistemas de ecuaciones e indicar si son compatibles (determinados

o indeterminados) e incompatibles.

a) {𝒙 + 𝟑𝒚 = 𝟕

−𝒙 + 𝟒𝒚 = 𝟕 e) {

𝟑𝒚 = 𝒙 − 𝟐𝟑𝒙 = 𝟔 + 𝟗𝒚

b) {𝒚 − 𝒙 = 𝟒

𝒙 + 𝟐𝒚 = 𝟐 f) {

9𝑥 − 3𝑦 = 156𝑥 − 2𝑦 = 10

c) {𝒙 − 𝟑 = 𝒚

𝟐𝒙 − 𝟐𝒚 = −𝟔 g) {

𝑥 + 𝑦 = 92𝑥 − 𝑦 = −3

d) {𝟏, 𝟑𝒙 − 𝟎, 𝟐𝒚 = 𝟏𝟐𝟎, 𝟒𝒙 + 𝟏𝟕𝒚 = 𝟖𝟗

h) {0,3𝑥 + 0.2𝑦 = 0,3

0,3 𝑥 + 0,3𝑦 = −0,2

Actividad Nº 6

Encuentra la solución, cuando sea posible, a los siguientes sistemas de ecuaciones, utilizando el método gráfico.

a) y – x = 1 b) 2x + 4y = 6 c) y + 2x + 8 = 0

x + y = 3 2y + x – 3 = 0 x + 1

2y = 2

Sistema de tres ecuaciones lineales con tres incógnitas

Un sistema de tres ecuaciones con tres incógnitas tiene la forma:

a1𝑥 + b1𝑦 + c1𝑧 = d

a2𝑥 + b2𝑦 + c2𝑧 = e donde a1, a2, a3, b1, b2, b3, c1, c2, c3, son los coeficientes de

a3𝑥 + b3𝑦 + c3𝑧 = f las incógnitas, d, e y f son los términos independientes.

Todos los coeficientes y términos independientes pertenecen al conjunto de números

reales.

Resolver un sistema de tres ecuaciones lineales con tres incógnitas es hallar la intersección

de los conjuntos solución de las ecuaciones que lo forman. La solución es una terna

ordenada ( 𝑥, 𝑦, 𝑧).


12

Para resolver un sistema de tres ecuaciones lineales con tres incógnitas, también

podríamos aplicar cualquiera de los métodos vistos para un sistema de dos ecuaciones con

dos incógnitas.

La gráfica de una ecuación lineal en dos variables es una recta mientras que, la de una

ecuación lineal en tres variables es un plano. Es decir, si un sistema de ecuaciones de tres

variables tiene solución única, esta será correspondiente a un punto en común a todos los

planos.

Ejemplos:

a) {

𝑥 + 𝑦 + 𝑧 = 32𝑥 + 𝑦 + 𝑧 = 4

𝑥 + 2𝑦 − 3𝑧 = 0

Método de Determinantes

Resolvemos el sistema por el método de determinantes. Aplicamos determinantes de

tercer orden, es decir, tres filas por tres columnas (3x3). Para encontrar el determinante general

y los de cada variable aplicamos la regla de Sarrus, para ello se agregan como 4º y 5º filas la

repetición de la 1º y 2º:

∆= ||

1 1 12 1 1

1 2 − 3𝟏 𝟏 𝟏𝟐 𝟏 𝟏

|| = 1.1.(-3) + 2.2.1 + 1.1.1−(1.1.1 + 1.2.1+ (-3).1.2)= -3 + 4 + 1 – (1 + 2 – 6) = 2 – (−3) = 5

∆x= ||

3 1 14 1 1

0 2 − 3𝟑 𝟏 𝟏𝟒 𝟏 𝟏

|| = 3.1. (-3) + 4.2.1 + 0.1.1 – (1.1.0 + 1.2.3 + (-3).1.4) = -9 + 8 + 0 – (0 + 6 – 12) = −1 +6= 5

∆y = ||

1 3 12 1 11 0 − 3𝟏 𝟑 𝟏𝟐 𝟏 𝟏

||= 1.1. (-3) + 2.0.1 + 1.3.1−(1.1.1 + 1.0.1+ (-3).3.2)= -3 + 0 + 3 – (1 + 0 – 18) = 0 – (−3) = 5

∆z = ||

1 1 32 1 41 2 0𝟏 𝟏 𝟑𝟐 𝟏 𝟒

|| = 1.1.0 + 2.2.3 + 1.1.4−(3.1.1 + 4.2.1+ 0.1.2)= 0 + 12 + 4 – (3 + 8 +0) = 16 – 11 = 5

𝑥 = △𝑥

△=> 𝑥 =

5

5 => 𝒙 = 𝟏 ; 𝑦 =

△𝑦

△=> 𝑦 =

5

5=> 𝒚 = 𝟏 ∶ 𝑧 =

△𝑧

△=> 𝑧 =

5

5=> 𝒛 = 𝟏

El sistema es compatible determinado (S.C.D), tiene solución única Solución: {(1; 1; 1)}

b) {

3𝑥 − 2𝑦 + 𝑧 = 26𝑥 − 4𝑦 + 2𝑧 = 19𝑥 − 6𝑦 + 3𝑧 = 3


13

∆=||

3 − 2 16 − 4 29 − 6 3𝟑 − 𝟐 𝟏𝟔 − 𝟒 𝟐

||=3.(-4).3 + 6.(-6).1 + 9.(-2).2−(1.(-4).9 + 2.(-6).3+ 3.(-2).6= -36 - 36 -36–(-36 -36 -36)=-108+108 = 0

∆x =||

2 − 2 11 − 4 23 − 6 3𝟐 − 𝟐 𝟏𝟏 − 𝟒 𝟐

||=2.(-4).3 + 1.(-6).1 + 3. (-2).2−(1. (-4).3 + 2. (-6).2+ 3. (-2).1)=-24 - 6 -12– (-12 -24 -6) = -42+42 =0

∆y = ||

3 2 1

6 1 2

9 3 3

𝟑 𝟐 𝟏

𝟔 𝟏 𝟐

||= 3.1.3 + 6.3.1 + 9.2.2−(1.1.9 + 2.3.3+ 3.2.6)= 9 +18 +36 – (9 +18 +36) = 63 - 63 = 0

∆z =||

3 − 2 26 − 4 19 − 6 3𝟑 − 𝟐 𝟐𝟔 − 𝟒 𝟏

||=3.(-4).3 + 6.(-6).2 + 9.(-2).1−(2.(-4).9 +1.(-6).3+ 3.(-2).6)=-36 - 72 -18–(-72 -18 -36)=-126+126 =0

Todos los determinantes dan cero, por lo tanto el sistema admite infinitas soluciones. El sistema

es compatible indeterminado (S.C.I)

c) {

𝑥 + 4𝑦 + 3𝑧 = 1𝑥 + 2𝑦 + 𝑧 = −52𝑥 + 4𝑦 + 2𝑧 = 0

∆= ||

1 4 3 1 2 1 2 4 2 𝟏 𝟒 𝟑 𝟏 𝟐 𝟏

||=1.2.2 + 1.4.3+ 2.4.1−(3.2.2 +1.4.1+ 2.4.1)= 4 +12 +8–(12 + 4 +8)=24-24 = 0

∆x=||

1 4 3−5 2 1 0 4 2 𝟏 𝟒 𝟑−𝟓 𝟐 𝟏

||= 1.2.2+(-5).4.3 +0.4.1 – (3.2.0 +1.4.1 + 2.4.(-5)) =4-60+0 – (0+4-40) = -56 +36 = -20

∆y= ||

1 1 3 1 − 5 1 2 0 2 𝟏 𝟏 𝟑𝟏 − 𝟓 𝟏

||=1.(-5).2 + 1.0.3+ 2.1.1−(3.(-5).2 +1.0.1+ 2.1.1)= -10 +0 +2–(-30 + 0 +2)=-8+28 =-20

∆z= ||

1 4 1 1 2 − 5 2 4 0 𝟏 𝟒 𝟏

𝟏 𝟐 − 𝟓

||=1.2.0 + 1.4.1+ 2.4.(-5)−(1.2.2 +(-5).4.1+ 0.4.1)= 0 +4 - 40–(4 -20 +0)=-36+16 = -20

Sólo el determinante general es igual a cero, por lo tanto, el sistema no tiene solución. Sistema

Incompatible. (S.I)


14

Método de Sustitución

a) {

𝑥 + 𝑦 + 𝑧 = 32𝑥 + 𝑦 + 𝑧 = 4

𝑥 + 2𝑦 − 3𝑧 = 0

1º- Despejamos una incógnita de una de las ecuaciones (elegimos 𝑥 de la primera ecuación)

𝑥 + 𝑦 + 𝑧 = 3 => 𝑥 = 3 − 𝑦 − 𝑧 (1)

2º- Reemplazamos en las otras ecuaciones la incógnita despejada, transformando un sistema de tres

ecuaciones con tres incógnitas en uno de dos ecuaciones con dos incógnitas y operamos.

2. (3 − 𝑦 − 𝑧) + 𝑦 + 𝑧 = 4 6 −2𝑦 − 2𝑧 + 𝑦 + 𝑧 = 4 −𝑦 − 𝑧 = −2

3 − 𝑦 − 𝑧 + 2𝑦 − 3𝑧 = 0 3 − 𝑦 − 𝑧 + 2𝑦 − 3𝑧 = 0 𝑦 − 4𝑧 = −3

3º- Elegimos 𝑦 en la segunda ecuación y la despejamos. Luego, reemplazamos en la primera ecuación

la 𝑦, por la expresión encontrada. 𝑦 − 4𝑧 = −3 => 𝑦 = −3 + 4𝑧 (2)

Reemplazamos en −𝑦 − 𝑧 = −2 queda: −(−3 + 4𝑧) − 𝑧 = −2 => 3 − 4𝑧 − 𝑧 = −2 =>

−5𝑧 = −2 − 3 => 𝑧 = −5: (−5) => 𝒛 = 𝟏

4º- Se reemplaza el valor de la incógnita hallada en (2) y luego ambas en (1)

(2) 𝑦 = −3 + 4𝑧 => 𝑦 = −3 + 4. (1) => 𝑦 = −3 + 4 => 𝒚 = 𝟏

(1) 𝑥 = 3 − 𝑦 − 𝑧 => 𝑥 = 3 − 1 − 1 => 𝒙 = 𝟏

Solución: {(1; 1;1)}

b) {

3𝑥 − 2𝑦 + 𝑧 = 26𝑥 − 4𝑦 + 2𝑧 = 19𝑥 − 6𝑦 + 3𝑧 = 3

1º- Despejamos una incógnita de una de las ecuaciones (elegimos 𝑧 de la primera ecuación)

𝑥 + 𝑦 + 𝑧 = 2 => 𝑧 = 2 − 3𝑥 + 2𝑦 (1)

2º- Reemplazamos en las otras ecuaciones la incógnita despejada (1), transformando un sistema

de tres ecuaciones con tres incógnitas en uno de dos ecuaciones con dos incógnitas y operamos.

6𝑥 − 4𝑦 + 2(2 − 3𝑥 + 2𝑦) = 1 6𝑥 − 4𝑦 + 4 − 6𝑥 + 4𝑦 = 1 0 = -3

9𝑥 − 6𝑦 + 3(2 − 3𝑥 + 2𝑦) = 3 9𝑥 − 6𝑦 + 6 − 9𝑥 + 6𝑦 = 3 0 = -3

Se han anulado las incógnitas y obtenemos 0 = -3 en ambas expresiones, esto es un absurdo.

El sistema admite infinitas soluciones. Es compatible indeterminado. (S.C.I)

c) {

𝑥 + 4𝑦 + 3𝑧 = 1𝑥 + 2𝑦 + 𝑧 = −52𝑥 + 4𝑦 + 2𝑧 = 0


15

1º- Despejamos una incógnita de una de las ecuaciones (elegimos 𝑥 de la primera ecuación)

𝑥 + 4𝑦 + 3𝑧 = 1 => 𝑥 = 1 − 4𝑦 − 3𝑧 (1)

2º- Reemplazamos en las otras ecuaciones la incógnita despejada, transformando un sistema

de tres ecuaciones con tres incógnitas en uno de dos ecuaciones con dos incógnitas y operamos.

1 − 4𝑦 − 3𝑧 + 2𝑦 + 𝑧 = −5 −2𝑦 − 2𝑧 = −6 −2𝑦 − 2𝑧 = −6

2(1 − 4𝑦 − 3𝑧) + 4𝑦 + 2𝑧 = 0 2 − 8𝑦 − 6𝑧 + 4𝑦 + 2𝑧 = 0 −4𝑦 − 4𝑧 = −2

3º- Elegimos 𝑦 en la primera ecuación y la despejamos. Luego, reemplazamos en la segunda ecuación

la 𝑦, por la expresión encontrada.

−2𝑦 − 2𝑧 = −6 => 𝑦 = 3 − 𝑧 (2)

Reemplazamos en −4𝑦 − 4𝑧 = −2 y queda: −4(3 − 𝑧) − 4𝑧 = −2 => −12 + 4𝑧 − 4𝑧 = −2 =>

=> 0 = −2 + 12 => 0 = 10 . Un absurdo, lo que indica que el sistema no tiene solución.

Es Incompatible. (S.I)

Método de Igualación

a) {

𝑥 + 𝑦 + 𝑧 = 32𝑥 + 𝑦 + 𝑧 = 4

𝑥 + 2𝑦 − 3𝑧 = 0

1º- Despejamos la misma variable en las tres ecuaciones

𝑥 + 𝑦 + 𝑧 = 3 => 𝑥 = 3 − 𝑦 − 𝑧 (1)

2𝑥 + 𝑦 + 𝑧 = 4 => 2𝑥 + 𝑦 + 𝑧 => 𝑥 =4−𝑦−𝑧

2 (2)

𝑥 + 2𝑦 − 3𝑧 = 0 => 𝑥 = −2𝑦 + 3𝑧 (3)

2º- De [1] y [2] y de [1] y [3] resulta igualando los segundos miembros:

3 − 𝑦 − 𝑧 =4−𝑦−𝑧

2 (1’) 3 − 𝑦 − 𝑧 = −2𝑦 + 3𝑧 (2’)

3º- Trasponiendo términos y reduciendo los que son semejantes, se obtiene en cada caso:

2. (3 − 𝑦 − 𝑧) = 4 − 𝑦 − 𝑧 3 − 𝑦 − 𝑧 = −2𝑦 + 3𝑧

6 − 2𝑦 − 2𝑧 = 4 − 𝑦 − 𝑧 −𝑦 + 2𝑦 − 𝑧 − 3𝑧 = −3

−2𝑦 + 𝑦 − 2𝑧 + 𝑧 = 4 − 6 𝑦 − 4𝑧 = −3 [B]

−𝑦 − 𝑧 = −2 [A]

4º- Llegamos así, de un sistema de tres ecuaciones con tres incógnitas, a otro de dos

ecuaciones con dos incógnitas, del que despejaremos y en ambas ecuaciones:


16

−𝑦 − 𝑧 = −2 => 𝑦 = 2 − 𝑧

𝑦 − 4𝑧 = −3 => 𝑦 = −3 + 4𝑧

5º- Igualamos los segundos miembros de ambas expresiones y de esta manera encontramos el

valor de 𝒛, que luego sustituimos en cualquiera de las 𝒚 despejada.

2 − 𝑧 = −3 + 4𝑧 => −𝑧 − 4𝑧 = −3 − 2 => −5𝑧 = −5 => 𝑧 = −5: (−5) => 𝒛 = 𝟏

𝑦 = 2 − 𝑧 => 𝑦 = 2 − 1 => 𝒚 = 𝟏

6º- Estos valores encontrados los sustituidos en (1), (2) o (3), para encontrar el valor de la

incógnita que falta averiguar, en este caso, 𝑥.

(1) 𝑥 = 3 − 𝑦 − 𝑧 => 𝑥 = 3 − 1 − 1 => 𝒙 = 𝟏 Solución: {(1; 1; 1)}

b) {

3𝑥 − 2𝑦 + 𝑧 = 26𝑥 − 4𝑦 + 2𝑧 = 19𝑥 − 6𝑦 + 3𝑧 = 3

1º- 𝑧 = 2 + 2𝑦 − 3𝑥 (1)

𝑧 =1−6𝑥+4𝑦

2 (2)

𝑧 =3−9𝑥+6𝑦

3 (3)

Igualamos la primera ecuación con segunda y la tercera.

2º- 2 + 2𝑦 − 3𝑥 = 1−6𝑥+4𝑦

2 2 + 2𝑦 − 3𝑥 =

3−9𝑥+6𝑦

3

4+4𝑦 − 6𝑥 = 1 − 6𝑥 + 4𝑦 6 + 6𝑦 − 9𝑥 = 3 − 9𝑥 + 6𝑦

4𝑦 − 4𝑦 − 6𝑥 + 6𝑥 = 1 − 4 6𝑦 − 6𝑦 − 9𝑥 + 9𝑥 = 3 − 6

0 = −3 0 = −3

En ambos casos se anulan las incógnitas nos que 0=-3, un absurdo. El sistema admite infinitas

soluciones. Es compatible indeterminado. (S.C.I)

c)

𝑥 + 4𝑦 + 3𝑧 = 1𝑥 + 2𝑦 + 𝑧 = −52𝑥 + 4𝑦 + 2𝑧 = 0

1º- 𝑥 = 1 − 4𝑦 − 3𝑧 (1)

𝑥 = −2𝑦 − 𝑧 − 5 (2)

𝑥 =−4𝑦−2𝑧

2 (3)


17

2º- 1 − 4𝑦 − 3𝑧 = −2𝑦 − 𝑧 − 5 1 − 4𝑦 − 3𝑧 =−4𝑦−2𝑧

2

3º- −4𝑦 − 3𝑧 + 2𝑦 + 𝑧 = −5 − 1 2 − 8𝑦 − 6𝑧 = −4𝑦 − 2𝑧

−2𝑦 − 2𝑧 = −6 −4𝑦 − 4𝑧 = −2

4º- −2𝑦 − 2𝑧 = −6 => 𝑦 = 2𝑧−6

−2

−4𝑦 − 4𝑧 = −2 => 𝑦 =4𝑧−2

−4

2𝑧−6

−2=

4𝑧−2

−4 => −4(2𝑧 − 6) = −2(4𝑧 − 2) => −8𝑧 + 24 = −8𝑧 + 4 => 24 = 4

Se anulan las incógnitas, el sistema no tiene solución. Sistema incompatible (S.I)

Actividad Nº7

Indica si alguno de los siguientes sistemas de ecuaciones tiene una única solución.

a) {

𝑥 + 2𝑦 − 𝑧 = 13𝑥 − 𝑦 + 2𝑧 = 14𝑥 + 𝑦 + 𝑧 = 2

b) {

𝑥 + 2𝑦 − 3𝑧 = 12−2𝑥 + 5𝑦 − 𝑧 = 158𝑥 − 𝑦 + 4𝑧 = −22

c) {

2𝑥 − 𝑦 + 3𝑧 = −143𝑥 − 𝑦 − 𝑧 = −4

−𝑥 − 𝑦 + 15𝑧 = −40 d) {

2𝑥 + 𝑦 + 𝑧 = 8−3𝑥 − 2𝑦 − 𝑧 = 10

−𝑦 + 𝑧 = 44

Ecuación de la recta que pasa por un punto dada la pendiente

Si conocemos la pendiente m de una recta A y las coordenadas de uno de sus puntos, p

(𝑥1; 𝑦1), hallamos la ecuación de la recta de la siguiente manera: 𝑦 – 𝑦1 = 𝑚. (𝑥 – 𝑥1)

Ejemplos:

Encuentra la ecuación de la recta que pasa por p (2; 5) y cuya pendiente es 3.

𝑦 − 5 = 3. (𝑥 – 2) => 𝑦 = 3𝑥 − 6 + 5 => 𝒚 = 𝟑𝒙 − 𝟏

Hallar la ecuación de la recta que pasa por p(-1;-2) y cuya inclinación es ᾳ = 45º.

Tg45º = 1 𝑦 + 2 = 1. (𝑥 + 1) => 𝑦 = 𝑥 + 1 − 2 => 𝒚 = 𝒙 − 𝟏

Ecuación de la recta que pasa por dos puntos

La ecuación de cualquier recta no vertical que pasa por los puntos (𝑥1, 𝑦1) y (𝑥2; 𝑦2) se

calcula con la fórmula: 𝑦 − 𝑦1 = 𝑦2−𝑦1

x2−x1 . ( 𝑥 − 𝑥1)

Ejemplo: Encuentra la ecuación de la recta que pasa por p (2:5) y q (3;1)

𝑦 − 5 = 1−5

3−2 . ( 𝑥 − 2) => 𝑦 − 5 = −4. (𝑥 − 2) => 𝑦 = −4. 𝑥 + 8 + 5) => 𝒚 = −𝟒. 𝒙 + 𝟏𝟑

Rectas paralelas y perpendiculares

Dos rectas resultan paralelas cuando tienen la misma pendiente.

𝑦1 = 𝑚1𝑥 + 𝑏. 𝑦2 = 𝑚2𝑥 + 𝑐

Para que resulte 𝑦1 // 𝑦2 debe suceder 𝑚1= 𝑚2

Ejemplo: 𝑦 = 3𝑥 + 5 y 𝑦 = 3𝑥 − 8

Dos rectas resultan perpendiculares cuando tienen la pendiente invertida y de signo

contrario.


18

𝑦1 = 𝑚1𝑥 + 𝑏. 𝑦2 = 𝑚2𝑥 + 𝑐

Para que resulte 𝑦1 ⊥ 𝑦2 debe suceder 𝑚1= −1

𝑚2

Ejemplo: 𝑦 = −3𝑥 + 5 y 𝑦 = 1

3𝑥 − 8

Actividad Nº8

a) Encuentra la ecuación de la recta que corresponde a cada gráfico.

b) Da un ejemplo de recta paralela y perpendicular para cada una de ellas.

Actividad Nº9

a) Encuentra la ecuación de la recta que pasa por el punto p (-3; 5) y cuya pendiente es 1

2

b) Determinar la ecuación de la recta que pasa por el punto q (6; -2) y tiene pendiente igual a -3. c) ¿Cuál es la ecuación de la recta que pasa por el punto r (-2;-4) y cuya inclinación es ᾳ = 135º?

d) Hallar las ecuaciones de la recta R que pasa por los puntos p (-5; 2) y n(-8;4) y de la recta T que pasa por los puntos p (0;3) y p(-3;4).

e) Encuentra la ecuación de la recta R, que pasa por el punto (8;3) y es paralela a la recta de

ecuación y = 2x – 3

f) Encuentra el valor de “k” de modo que las gráficas de 5𝑦 = 𝑘𝑥 + 3 y 1

4𝑦 =

1

10 𝑥 − 2 sean

paralelas

g) Determina la ecuación de la recta S que pasa por el punto p(2;4) y es paralela a T, ésta

última contiene a los puntos a(3;2) y b(4;5)

h) Halla la ecuación de la recta R, paralela a y =- 5

4 x + 2 y que pasa por el origen de

coordenadas.

i) Encontrar la recta N, perpendicular a la recta cuya ecuación es -2 + y – 4x = 0 y contiene al

punto a(3;-2)

j) La recta Q que pasa por el punto p (- 1

2;

1

2) es perpendicular a la recta V que contiene a los

puntos v (1;-1) y w (3

4; 0). Determina la ecuación de Q y de V.

Bibliografía

Marina E Andrés- Pablo J Kaczor – María C Latorre – Gustavo E Piñeiro- Gisela B Serrano Editorial Santillana Matemática III

Martín Pérez – Gabriela Righetti – Gustavo E Piñeiro- Gisela B Serrano Editorial Nuevamente Santillana Matemática III

Silvia Altman – Mabel Arnejo – Claudia Comparatore Editorial Tinta Fresca matemática ES3

Stanley A Smith – Randall I. Charles – John A. Dossey – Mervin L. Keedy – Marvin L. Bittinger. Álgebra y Trigonometría. Red federal de Formación Docente Continua

Ministerio de Cultura y Educación de la Nación. Addison Wesley Longman


19

MÓDULO V SISTEMA DE ECUACIONES FUNCIONES · 2019. 8. 22. · Solución :{(4:2)} Método de...

Documents

Transcript of MÓDULO V SISTEMA DE ECUACIONES FUNCIONES · 2019. 8. 22. · Solución :{(4:2)} Método de...