1 Unidad 1: la ecuacion de Burgers y el metodo

de Lax

1.1 La ecuacion de Burgers invıscida

La ecuacion de Burgers invıscida (o ecuacion de Riemann):

∂u

∂t+ u

∂u

∂x= 0 , (1)

tiene soluciones analıticas y numericas que han sido estudiadas extensamente.Es considerada como la ecuacion en derivadas parciales no lineales mas sen-cilla.

Por ejemplo, esta ecuacion admite la solucion discontinua :

u(x, t) = u1 , x < vst ,

= u2 , x > vst ,

con vs =u1 + u2

2. (2)

La ecuacion de Burgers puede ser escrita en “forma de conservacion” :

∂U

∂t+∂F

∂x= 0 , (3)

con U = u y F = u2/2. Generalmente, se busca escribir en esta “forma deconservacion” a las ecuaciones (por ejemplo, las de dinamica de gases o de lamagnetohidrodinamica) para aplicarles algoritmos de integracion numerica.

1.2 El metodo de Lax

El metodo de Lax es el metodo de diferencias finitas mas sencillo posiblepara integrar ecuaciones en forma de conservacion. Para aplicar este metodo,primero se discretiza la coordenada espacial x en la forma :

xi = i∆x ; i = 0, 1, ...N , (4)

con ∆x = xmax/N , donde xmax es el tamano del dominio computacional.La derivada espacial en la ecuacion (3) se discretiza como :(

∂F

∂x

)i

=Fi+1 − Fi−1

2∆x. (5)

Dada una solucion inicial u(x, t) (el valor de u a tiempo t para todo x–es decir para todos los xi–), primero calculamos Ui(t) = u(xi, t) y Fi(t) =u2(xi, t)/2. La soluci’on a un tiempo t+ ∆t sera calculada como :

Ui(t+ ∆t) =Ui−1(t) + Ui+1(t)

2−∆t

(∂F

∂x

)i

(t) . (6)

Combinando esta ecuacion con la ecuacion (5) entonces tenemos :

Ui(t+ ∆t) =Ui−1(t) + Ui+1(t)

2−∆t

Fi+1(t)− Fi−1(t)

2∆x. (7)

Aplicando (7) en forma recursiva “se avanza la solucion en el tiempo”, esdecir obtenemos la solucion para tiempos t+ 2∆t, t+ 3∆t, etc. .

Del llamado analisis de von Neumann (que veremos en detalle mas ade-lante en el curso) se deduce que para que este metodo sea estable, es necesarioelegir un paso del tiempo que cumpla la condicion :

∆t = Co×min

[∆x

ui

]i=0,...N

, (8)

con Co < 1 (numero de Courant menor que 1). Esta es la llamada “condicionCFL” (Courant, Friedrichs, Lewy). La derivacion del criterio de estabilidadpara el metodo de Lax esta hecha en la seccion 1.4.

1.3 Implementacion del metodo de Lax

Como primer problema de programacion del curso, implementaremos el metodode Lax para la ecuacion de Burgers para resolver el siguiente problema :

• un dominio computacional con x = 0→ 1, discretizado con N+1 = 201puntos,

• una condicion inicial (a t = 0) u = 2 para x ≤ 0.1 y u = 1 para x > 0.1.

A partir de esta condiciıon inicial, integraremos la ecuacion de Burgers conel metodo de Lax para obtener la solucion para tiempos t > 0.

En detalle, la implementacion debe tener los siguientes detalles :

1. poner ∆x = xmax/N = 1/N ,

2. poner ui = 2 para xi = i∆x < xc = 0.1 y ui = 1 para xi > xc,

3. en el punto xi mas cercano a xc (o sea, el punto que satisface lacondicion xi −∆x/2 ≤ xc < xi + ∆x/2) poner ui = (1 + 2)/2,

4. calcular Ui = ui y Fi = u2i /2,

5. calcular el paso en el tiempo ∆t con el criterio CFL tomando Co = 0.9(ecuacion 8),

6. usar el algoritmo de Lax para calcular U ′i = Ui(t + ∆t) (ecuacion 7)para i = 1, ...N − 1,

7. poner U ′0 = U0 (condicion “de entrada”) y U ′N = U ′N−1 (condicion “desalida”),

8. escribir a un archivo (xi, Ui), i = 1, ...N si se satisface la condiciont ≤ k∆tp ≤ t + ∆t (donde k = 0, 1, 2, ... y ∆tp = 0.02 es el intervalotemporal entre salidas),

9. poner ui = U ′i , t = t+ ∆t,

10. si la condicion t ≤ tmax = 0.7 es satisfecha, regresar al punto 4.

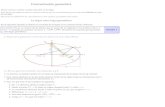
El codigo “clase1.f” realiza estas operaciones, y la figura 1 muestra lasolucion obtenida. La grafica ha sido hecha con el graficador “supermongo”(sm) usando el macro “clase1.sm”. Tambien est’a una version en fortran90 del programa (clase1.f90) y un script de gnuplot que permite ver unasecuencia de graficas generadas en el programa (clase1.gpl).

1.4 Analisis de von Neumann: estabilidad del metodode Lax

Para deducir la “condicion CFL” (ecuacion 8) se usa el llamado “analisis devon Neumann”. La idea de este analisis es escribir :

u = u+ ξ ; ξ � u , (9)

donde u es la solucion exacta (en nuestro caso, de la ecuacion de Burgers),y ξ es el error del calculo numerico (por ejemplo, el error por redondeo).Insertando (9) en (1), tenemos:

∂u

∂t+ u

∂u

∂x+∂ξ

∂t+ u

∂ξ

∂x+ ξ

∂ξ

∂x+ ξ

∂u

∂x= 0 . (10)

Figure 1: Solucion de la ecuacion de Burgers con el metodo de Lax, para lascondiciones iniciales de la seccion 1.3. Las curvas corresponded a intervalostemporales 5∆tp = 0.1.

La suma de los dos primeros terminos (en la izquierda de la ecuacion 10)es igual a cero (dado que u es la solucion exacta). El quinto termino escuadratico en ξ, y por lo tanto lo podemos despreciar.

Generalmente, el error ξ en una integracion numerica es de alta frecuen-cia (basicamente, con altas oscilaciones entre puntos sucesivos de la mallacomputacional). Entonces, supondremos que∣∣∣∣u∂ξ∂x

∣∣∣∣� ∣∣∣∣ξ ∂u∂x∣∣∣∣ . (11)

Con estas consideraciones, simplificamos la ecuacion (10) a:

∂ξ

∂t+ v

∂ξ

∂x= 0 , (12)

con v = u aproximadamente constante (dado que sus variaciones tienenescalas espaciales mucho mayores que las de ξ). O sea que el error ξ satisfaceuna ecuacion de onda lineal de primer orden.

Podemos escribir ξ como una suma de componentes de Fourier ∝ eikx, ycomo la ecuacion (12) es lineal, cada componente de Fourier debe satisfac-erla en forma independiente. Entonces, nos limitamos a estudiar el compor-tamiento de una componente de Fourier de ξ :

ξ(x, t) = eikx+nt , (13)

limitandonos a estudiar las soluciones con dependencia temporal exponencial.Si aplicamos el algoritmo de Lax (ecuacion 7) a la ecuacion (12) obten-

emos :

ξj(t+ ∆t) =ξj−1(t) + ξj+1(t)

2− v∆t

2∆x[ξj+1(t)− ξj−1(t)] , (14)

donde ξj = ξ(xj, t). Usando la ecuacion (13) podemos calcular

ξj(t+ ∆t) = ξj(t)en∆t , (15)

ξj+1(t) = ξj(t)eik∆x , (16)

ξj−1(t) = ξj(t)e−ik∆x , (17)

y substituyendo (15-17) en (14) obtenemos :

en∆t = cos k∆x+iv∆t

∆xsin k∆x . (18)

El llamado “factor de amplificacion” A se define como :

A ≡∣∣∣∣ξj(t+ ∆t)

ξj(t)

∣∣∣∣ =∣∣en∆t

∣∣ =

√cos2 k∆x+

(v∆t

∆x

)2

sin2 k∆x , (19)

donde para la seguna igualdad hemos usado la ecuacion (18).Es claro que si A < 1 el modulo del error decrece con el tiempo. Esta

condicion es el criterio de estabilidad del analisis de von Neumann. Dela ecuacion (19) vemos que el metodo de Lax es estable si se satisface lacondicion :

Co =v∆t

∆x< 1 . (20)