Inestabilidad inducida por rozamiento en un p¶endulo...

ESCUELA SUPERIOR DE INGENIEROS DE SEVILLA

UNIVERSIDAD DE SEVILLA

Departamento de Matematica Aplicada II

PROYECTO FIN DE CARRERA

Inestabilidad inducida

por rozamiento en un pendulo

esferico sometido a rotacion

Realizado por D. Emilio Garcıa Falantes

Directores del proyecto: Dr. D. Emilio Freire Macıas

y Dr. D. Fernando Fernandez Sanchez

Sevilla, Marzo de 2005

Indice general

1. Introduccion. 11.1. El pendulo de Furuta. . . . . . . . . . . . . . . . . . . . . . . 11.2. Objetivos del proyecto. . . . . . . . . . . . . . . . . . . . . . . 2

2. Ecuaciones de movimiento del sistema. 42.1. Modelo del sistema. . . . . . . . . . . . . . . . . . . . . . . . . 42.2. Ecuaciones diferenciales del modelo. . . . . . . . . . . . . . . . 5

2.2.1. Vector de posicion. . . . . . . . . . . . . . . . . . . . . 52.2.2. Vector de velocidad. . . . . . . . . . . . . . . . . . . . 52.2.3. Energıa cinetica. . . . . . . . . . . . . . . . . . . . . . 62.2.4. Energıa potencial. . . . . . . . . . . . . . . . . . . . . . 62.2.5. Energıa disipativa. . . . . . . . . . . . . . . . . . . . . 62.2.6. Ecuaciones de Lagrange. . . . . . . . . . . . . . . . . . 72.2.7. Ecuaciones diferenciales adimensionalizadas. . . . . . . 10

2.3. Ecuaciones de equilibrio. . . . . . . . . . . . . . . . . . . . . . 10

3. Continuacion numerica de equilibrios. 183.1. Introduccion. . . . . . . . . . . . . . . . . . . . . . . . . . . . 183.2. Funcionamiento de AUTO2000. . . . . . . . . . . . . . . . . . 203.3. Continuacion numerica de las ecuaciones de nuestro modelo. . 25

3.3.1. Calculo de equilibrios . . . . . . . . . . . . . . . . . . . 253.3.2. Continuacion de los equilibrios. . . . . . . . . . . . . . 283.3.3. Continuacion del punto lımite (LP). . . . . . . . . . . . 393.3.4. Continuacion del punto Hopf-Zero (HZ). . . . . . . . . 463.3.5. Estabilidad e inestabilidad. Espectro de autovalores. . . 54

3.4. Conclusiones sobre la continuacion numerica de los equilibrios. 64

4. Continuacion numerica de orbitas periodicas. 664.1. Introduccion. . . . . . . . . . . . . . . . . . . . . . . . . . . . 664.2. Algunas nociones sobre AUTO2000. . . . . . . . . . . . . . . . 664.3. Continuacion de orbitas periodicas a partir de puntos de Hopf. 68

i

4.3.1. Continuacion de los puntos de Hopf contenidos en lahorizontal de valor µ = 0,58. . . . . . . . . . . . . . . . 69

4.3.2. Continuacion de los puntos de Hopf contenidos en lahorizontal de valor µ = 0,69. . . . . . . . . . . . . . . . 71

4.3.3. Continuacion del punto de Hopf contenido en la hori-zontal de valor µ = 0,9. . . . . . . . . . . . . . . . . . . 75

5. Conclusiones. 78

Bibliografıa 81

ii

Indice de figuras

1.1. Pendulo de Furuta. . . . . . . . . . . . . . . . . . . . . . . . . 11.2. Modelo del pendulo de Furuta. . . . . . . . . . . . . . . . . . . 2

2.1. Modelo del sistema. . . . . . . . . . . . . . . . . . . . . . . . . 42.2. Primera clase de equilibrio. . . . . . . . . . . . . . . . . . . . . 112.3. Segunda clase de equilibrio. . . . . . . . . . . . . . . . . . . . 122.4. Tercera clase de equilibrio. . . . . . . . . . . . . . . . . . . . . 132.5. Parametro ν variando. . . . . . . . . . . . . . . . . . . . . . . 152.6. Parametro µ variando. . . . . . . . . . . . . . . . . . . . . . . 162.7. Solucion de la ecuacion aproximada.. . . . . . . . . . . . . . . 17

3.1. Ejecucion de AUTO. . . . . . . . . . . . . . . . . . . . . . . . 243.2. Primera clase de equilibrio. . . . . . . . . . . . . . . . . . . . . 263.3. Segunda clase de equilibrio. . . . . . . . . . . . . . . . . . . . 273.4. Segunda clase de equilibrio. . . . . . . . . . . . . . . . . . . . 283.5. Ejecucion del fichero “equi1”. . . . . . . . . . . . . . . . . . . 303.6. ϕ frente a µ de un equilibrio tipo 1 con ν = 0,7. . . . . . . . . 313.7. θ frente a µ de un equilibrio tipo 1 con ν=0.7. . . . . . . . . . 323.8. Espectro de autovalores para el fichero ‘c.equi1’. . . . . . . . . 333.9. ϕ frente a µ de un equilibrio tipo 2 con ν = 0,7. . . . . . . . . 343.10. θ frente a µ de un equilibrio tipo 2 con ν=0.7. . . . . . . . . . 353.11. Espectro de autovalores para el fichero ‘c.equi2’. . . . . . . . . 353.12. ϕ frente a µ de un equilibrio tipo 3 con ν = 0,7. . . . . . . . . 363.13. θ frente a µ de un equilibrio tipo 3 con ν=0.7. . . . . . . . . . 373.14. Autovalores en el punto lımite (LP). . . . . . . . . . . . . . . 383.15. Espectro de autovalores a ambos lados del LP. . . . . . . . . . 383.16. Continuacion del LP para valores decrecientes de µ. . . . . . . 413.17. Curva completa de LP. . . . . . . . . . . . . . . . . . . . . . . 423.18. Puntos destacados en la curva LP. . . . . . . . . . . . . . . . . 433.19. Autovalores en la rama 1 del LP. . . . . . . . . . . . . . . . . 443.20. Autovalores en la rama 2 del LP. . . . . . . . . . . . . . . . . 453.21. Vertical trazada para ν = 0,163. . . . . . . . . . . . . . . . . . 47

iii

3.22. Vertical trazada para ν = 0,163. . . . . . . . . . . . . . . . . . 483.23. Curva de Hopf para la solucion II. . . . . . . . . . . . . . . . . 503.24. Espectro de autovalores en el punto Hopf-Zero. . . . . . . . . . 513.25. Espectro de autovalores de la curva de Hopf perteneciente a

la solucion II. . . . . . . . . . . . . . . . . . . . . . . . . . . . 513.26. Curva de Hopf para la solucion III. . . . . . . . . . . . . . . . 523.27. Espectro de autovalores de la curva de Hopf perteneciente a

la solucion III. . . . . . . . . . . . . . . . . . . . . . . . . . . . 533.28. Corte vertical con ν = 0,163. . . . . . . . . . . . . . . . . . . . 543.29. Cortes horizontales para valores de µ constantes. . . . . . . . . 553.30. Corte horizontal para µ = 0,29. . . . . . . . . . . . . . . . . . 563.31. Espectro de autovalores en el corte horizontal con valor µ = 0,29. 573.32. Corte horizontal para µ = 0,58. . . . . . . . . . . . . . . . . . 583.33. Espectro de autovalores en el corte horizontal con valor µ = 0,58. 593.34. Corte horizontal para µ = 0,58. . . . . . . . . . . . . . . . . . 603.35. Corte horizontal para µ = 0,69. . . . . . . . . . . . . . . . . . 613.36. Espectro de autovalores en el corte horizontal con valor µ = 0,69. 623.37. Corte horizontal para µ = 0,9. . . . . . . . . . . . . . . . . . . 633.38. Espectro de autovalores en el corte horizontal con valor µ = 0,9. 64

4.1. Puntos de Hopf a partir de los que se continuaran las orbitasperiodicas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

4.2. Orbita periodica correspondiente a µ = 0,58. . . . . . . . . . . 694.3. Multiplicadores para la orbita periodica con µ = 0,58. . . . . . 704.4. Orbita periodica correspondiente a µ = 0,69. . . . . . . . . . . 714.5. Multiplicadores para la orbita periodica con µ = 0,69. . . . . . 724.6. Representacion del angulo ϕ frente a θ para la orbita periodica

con µ = 0,69. . . . . . . . . . . . . . . . . . . . . . . . . . . . 744.7. Orbita periodica con µ = 0,69 en coordenadas cartesianas. . . 754.8. Orbita periodica correspondiente a µ = 0,9. . . . . . . . . . . . 764.9. Multiplicadores para la orbita periodica con µ = 0,9. . . . . . 77

5.1. Posicion de equilibrio con el pendulo cruzado. . . . . . . . . . 785.2. Posicion de equilibrio clasica. . . . . . . . . . . . . . . . . . . 795.3. Posicion de equilibrio con el pendulo invertido. . . . . . . . . . 80

iv

Capıtulo 1

Introduccion.

1.1. El pendulo de Furuta.

El pendulo de Furuta (Figura 1.1) es un sistema de dos grados de libertadrotacionales.

Figura 1.1: Pendulo de Furuta.

El primer elemento (brazo), tiene un giro alrededor de un eje perpendi-cular a la base, mientras que el segundo elemento (pendulo), se encuentracolocado en un extremo del brazo y su eje de giro es colineal al eje axial delbrazo, realizando un giro en un plano perpendicular al brazo. Este proceso esfuertemente no lineal y posee interesantes caracterısticas dinamicas que no

1

CAPITULO 1. INTRODUCCION. 2

estan presentes en los clasicos pendulos con movimiento lineal del pivot; porejemplo, presenta una bifurcacion tridente cuando el brazo del motor se rotaa velocidad constante, existiendo dos equilibrios a baja velocidad y cuatro aalta velocidad.

Un esquema del pendulo de Furuta lo podemos ver en la Figura 1.2. Enel, los grados de libertad vienen definidos por las variables q1 y q2.

Figura 1.2: Modelo del pendulo de Furuta.

El sistema objeto de nuestro estudio a lo largo del proyecto esta basadoen el desarrollo numerico de una modificacion del pendulo de Furuta con laparticularidad de tener una rotula en la union entre el brazo y el penduloque convierte el movimiento plano en un movimiento esferico y, ademas, noconsiderar la masa que representa dicha rotula, sino unicamente la que seencuentra en el extremo del pendulo.

El hecho de que nuestro pendulo sea esferico provoca una separacionde la masa con respecto al eje de giro (grado de libertad ϕ), ademas delconsiguiente retraso provocado por el rozamiento viscoso entre dicha masa yel aire (angulo θ).

Nuestro sistema, representado en la Figura 2.1, sigue teniendo dos gradosde libertad a pesar de que nuestro pendulo sea esferico. Ello es debido a queel grado de libertad q2 de la Figura 1.2 no lo consideramos, ya que el giroprovocado por el motor sobre el eje vertical sera una constante impuesta pornosotros (ωt).

1.2. Objetivos del proyecto.

El estudio del presente proyecto, constara de dos parte bien diferenciadas,una parte analıtica y otra numerica, aunque fundamentalmente nos basare-

CAPITULO 1. INTRODUCCION. 3

mos en esta ultima, ya que al tratarse de un sistema no conservativo (debidoa la existencia del rozamiento), cabe esperar que las ecuaciones diferencialessean bastante complejas, y mediante metodos analıticos podremos llegar aconclusiones cualitativas mas que cuantitativas.

Los objetivos del proyecto seran definidos a continuacion:

Obtener las ecuaciones de movimiento del sistema definido por nuestromodelo de la Figura 2.1, utilizando la formulacion lagrangiana.

A partir de las ecuaciones de movimiento, obtener las ecuaciones deequilibrio del sistema, y realizar un estudio analıtico de las mismas, enla medida de lo posible, para obtener resultados, al menos, cualitativos.

Calcular una solucion que cumpla las ecuaciones de equilibrio y que nospermita continuar numericamente los posibles equilibrios en funcion delos parametros que elijamos.

Aprender el manejo del software de continuacion numerica AUTO2000,el cual emplearemos ampliamente durante el desarrollo del proyecto.

Mediante el software de continuacion numerica escogido, desarrollar almaximo la estabilidad e inestabilidad de los equilibrios del sistema queestamos estudiando.

A partir del diagrama de equilibrios del modelo representativo de nues-tro sistema, obtener algunas soluciones periodicas estables e inestables,y representarlas graficamente en funcion de las coordenadas cartesia-nas, para obtener ası una mejor perspectiva de las mismas.

Capıtulo 2

Ecuaciones de movimiento delsistema.

En este capıtulo, mostraremos el modelo escogido para representar nues-tro sistema, ası como las coordenadas que emplearemos para su estudio, ylas ecuaciones que regiran su movimiento.

ϕ

θ

Ζ

X

Y

ωt b

l

Figura 2.1: Modelo del sistema.

2.1. Modelo del sistema.

El modelo escogido para el estudio de nuestro sistema, es un modelobasado en dos grados de libertad (ademas del tiempo, por supuesto) y en el

4

CAPITULO 2. ECUACIONES DE MOVIMIENTO DEL SISTEMA. 5

que se han realizado una serie de hipotesis las cuales iremos justificando.En primer lugar mostraremos un esquema grafico del modelo (Figura 2.1),

en el que se pueden observar los distintos parametros que emplearemos pos-teriormente en el desarrollo de las ecuaciones.

El sistema esta formado por dos barras, una de longitud b que permaneceen el plano horizontal y que gira en el mismo con una frecuencia constanteω, y otra de longitud ` que esta vinculada a la primera mediante una rotulaque le permite un movimiento esferico, y en cuyo extremo se encuentra lamasa m.

En nuestro modelo, tomaremos como hipotesis de partida que la masa mes puntual y que ninguna de las barras tiene masa, lo cual simplificara en granmedida el estudio de nuestro problema. Debido a las hipotesis anteriores, elrozamiento actuara unicamente sobre la masa puntual debido al contacto conel aire.

Como hemos dicho anteriormente, nuestro sistema vendra definido pordos grados de libertad ϕ y θ, los cuales definen respectivamente el anguloque separa a la barra de longitud ` de la vertical, y el angulo que existe entrela proyeccion horizontal de la barra de longitud ` y el eje que define la barrade longitud b.

2.2. Ecuaciones diferenciales del modelo.

En este apartado, hallaremos las ecuaciones diferenciales que rigen elmovimiento de nuestro modelo empleando las ecuaciones de Lagrange.

2.2.1. Vector de posicion.

Basandonos en los ejes cartesianos mostrados en la Figura 2.1, definiremosel vector de posicion de la masa m como:

x=b · cos(ωt) + l · sin ϕ · cos(ωt + θ)

y=b · sin(ωt) + l · sin ϕ · sin(ωt + θ)

z=−l · cos ϕ

(2.1)

2.2.2. Vector de velocidad.

Para obtener la velocidad de la masa m en coordenadas cartesianas, bastacon derivar las tres expresiones del vector de posicion (2.1) con respecto al


tiempo, resultando:

x=−bω · sin(ωt) + l · ϕ · cos ϕ · cos(ωt + θ)− l · (ω + θ) · sin ϕ · sin(ωt + θ)

y=bω · cos(ωt) + l · ϕ · cos ϕ · sin(ωt + θ) + l · (ω + θ) · sin ϕ · cos(ωt + θ)

z=l · ϕ · sin ϕ(2.2)

Ademas de la expresion vectorial de la velocidad, tambien calcularemosel cuadrado del modulo de la misma, ya que nos sera de utilidad cuandohallemos expresiones como la de la energıa cinetica. Dicho valor viene dadoen funcion de las velocidades cartesianas por v2 = x2 + y2 + y2. Su valor esel siguiente:

v2=l2 · ϕ2 + l2 · sin2 ϕ · (ω + θ)2 + 2 · blω · cos ϕ · sin θ · ϕ+2 · blω · sin ϕ · cos θ · (ω + θ) + b2ω2

(2.3)

2.2.3. Energıa cinetica.

La expresion de la energıa cinetica viene dada por T = 12·m · v2. Susti-

tuyendo la v2 por la expresion (2.3), obtenemos:

T=1

2·ml2 · ϕ2 +

1

2·ml2 · sin2 ϕ · (ω + θ)2 + mblω · cos ϕ · sin θ · ϕ

+mblω · sin ϕ · cos θ · (ω + θ) +1

2· b2mω2

(2.4)

2.2.4. Energıa potencial.

La energıa potencial varıa unicamente con la altura de m, ya que en elapartado (2.1), establecimos como hipotesis que las barras de nuestro modelono tenıan masa, y que la unica masa a considerar serıa m.

La expresion de la energıa potencial es V = m · g · h, donde la h es ladistancia vertical que separa la masa m del plano horizontal que contiene adicha masa en la posicion de reposo del pendulo, ya que hemos tomado dichoplano como origen de potencial. Consecuencia directa de tomar este origenes, que la energıa potencial siempre sera positiva. Su valor es el siguiente:

V = mgl · (1− cos ϕ) (2.5)

2.2.5. Energıa disipativa.

La energıa disipativa surge como consecuencia del rozamiento de la masam con el aire. Su expresion es muy similar a la de la energıa cinetica, salvo


que como constante de proporcionalidad emplea el coeficiente de rozamientoc en lugar de la masa m. Por tanto, su expresion es ED = 1

2· c · v2.

Sustituyendo la velocidad al cuadrado por su valor dado en la ecua-cion (2.3), obtenemos:

ED=1

2· cl2 · ϕ2 +

1

2· cl2 · sin2 ϕ · (ω + θ)2 + cblω · cos ϕ · sin θ · ϕ

+(cblω · sin ϕ · cos θ) · (ω + θ) + 12· b2cω2

(2.6)

2.2.6. Ecuaciones de Lagrange.

Una vez halladas las tres energıas que intervendran en las ecuaciones deLagrange, plantearemos nuestras ecuaciones de movimiento para cada uno denuestros grados de libertad ϕ y θ.

En primer lugar, calcularemos la funcion Lagrangiana, la cual viene defi-nida a partir de la energıa cinetica T, y de la energıa potencial V de la formaque sigue:

L = T − V (2.7)

Si desarrollamos la expresion anterior, obtenemos la Lagrangiana en fun-cion de nuestros grados de libertad ϕ y θ:

L=1

2·ml2 · ϕ2 +

1

2·ml2 · sin2 ϕ · (ω + θ)2 + mblω · cos ϕ · sin θ · ϕ

+mblω · sin ϕ · cos θ · (ω + θ) +1

2· b2mω2 −mgl · (1− cos ϕ)

(2.8)

En lugar de sustituir la Lagrangiana en las ecuaciones de Lagrange di-rectamente, hemos optado por escribir dichas ecuaciones en funcion de lasenergıas potencial y cinetica (ademas de la disipativa claro, que no hemosnombrado debido a que no pertenece a la Lagrangiana). Dicho esto, en laecuacion (2.9) podemos ver las las ecuaciones de Lagrange para una coorde-nada generalizada q:

d

dt

(∂L

∂q

)+

∂ED

∂q=

∂L

∂q=⇒ d

dt

(∂T

∂q

)+

∂ED

∂q− ∂T

∂q+

∂V

∂q= 0 (2.9)

Ahora particularizaremos la ecuacion (2.9) para nuestros dos grados delibertad ϕ y θ.


Grado de libertad ϕ

∂T

∂ϕ=ml2 · ϕ + mblω · cos ϕ · sin θ

d

dt

(∂T

∂ϕ

)=ml2 · ϕ−mblω · sin ϕ · sin θ · ϕ−mblω · cos ϕ · cos θ · θ

∂ED

∂ϕ=cl2 · ϕ + cblω · cos ϕ · sin θ

∂T

∂ϕ=ml2 · sin ϕ · cos θ ·

(ω − θ

)2

+ mblω · sin ϕ sin θ · ϕ

−mblω cos ϕ · cos θ ·(ω + θ

)

∂V

∂ϕ=mgl · sin ϕ

La ecuacion diferencial obtenida para el grado de libertad ϕ es:

0=ml2 · ϕ−mblω · sin ϕ · sin θ · ϕ−mblω · cos ϕ · cos θ · θ + cl2 · ϕ+cblω · cos ϕ · sin θ −ml2 · sin ϕ · cos θ ·

(ω + θ

)2

+ mblω · sin ϕ sin θ · ϕ−mblω cos ϕ · cos θ ·

(ω + θ

)+ mgl · sin ϕ

(2.10)

Grado de libertad θ

∂T

∂θ=ml2 · sin2 ϕ ·

(ω + θ

)+ mblω · sin ϕ · cos θ

d

dt

(∂T

∂θ

)=2 ·ml2 · sin ϕ · cos ϕ

(ω + θ

)· ϕ + ml2 · sin2 ϕ · θ

+mblω · cos ϕ · cos θ · ϕ−mblω · sin ϕ · sin θ · θ∂ED

∂θ=cl2 · sin2 ϕ

(ω + θ

)+ cblω · sin ϕ · cos θ


∂T

∂θ=mblω · cos ϕ · cos θ · ϕ−mblω · sin ϕ · sin θ ·

(ω + θ

)

∂V

∂ϕ=0

La ecuacion diferencial obtenida para el grado de libertad θ es:

0=2 ·ml2 · sin ϕ · cos ϕ(ω + θ

)· ϕ + ml2 · sin2 ϕ · θ + cblω · sin ϕ · cos θ

−mblω · sin ϕ · sin θ · θ + cl2 · sin2 ϕ(ω + θ

)+ mblω · cos ϕ · cos θ · ϕ

−mblω · cos ϕ · cos θ · ϕ + mblω · sin ϕ · sin θ ·(ω + θ

)

(2.11)

Las ecuaciones de Lagrange nos han permitido obtener las dos ecuacionesde movimiento (2.10) y (2.11) correspondientes a los dos grados de libertadϕ y θ. En dichas ecuaciones, se pueden simplificar terminos semejantes, ob-teniendo finalmente las dos ecuaciones de movimiento de segundo orden queregiran nuestro sistema:

0=ϕ− sin ϕ · cos ϕ ·(ω + θ

)2

− bω2

l· cos ϕ · cos θ +

g

l· sin ϕ

+c

m· ϕ +

cbω

ml· cos ϕ · sin θ

(2.12)

0=θ · sin ϕ + 2 · cos θ ·(ω + θ

)· ϕ +

bω2

l· sin θ

+c

m· sin ϕ ·

(ω + θ

)+

cbω

ml· cos θ

(2.13)

Los dos ultimos terminos de las ecuaciones (2.12) y (2.13), representanla aportacion del rozamiento al problema, y son los responsables de que elgrado de libertad θ no valga cero en todo instante, sino que por el contrario,la masa m tenga un cierto retraso con respecto al plano vertical que contienea la barra de longitud b.


2.2.7. Ecuaciones diferenciales adimensionalizadas.

El siguiente paso que realizaremos, sera adimensionalizar las ecuacio-nes (2.12) y (2.13), para lo cual definiremos a continuacion los tres parametrosadimensionales que utilizaremos.

Relacion de frecuencias µ =

√g

l

ω.

En este parametro comparamos la frecuencia natural del pendulo√

gl

con la frecuencia de giro del sistema ω.

Relacion de brazos ν =b

l.

En este parametro comparamos las longitudes de los dos brazos delsistema, el horizontal de longitud b y el del pendulo de longitud `.

Rozamiento λ =c

mω.

Este parametro representa el rozamiento entre la masa m y el aire deforma adimensional.

Adimensionalizando las ecuaciones (2.12) y (2.13) y escalando el tiempocon ω, obtenemos las ecuaciones de movimiento de segundo orden adimen-sionalizadas, que seran las que empleemos en el siguiente apartado dedicadoa los equilibrios.

2.3. Ecuaciones de equilibrio.

Una vez obtenidas las ecuaciones de movimiento adimensionalizadas, pa-saremos a calcular las ecuaciones que regiran los distintos puntos de equilibriode nuestro sistema. Para ello, la unica condicion que habremos de imponeres que las coordenadas generalizadas empleadas en nuestras ecuaciones ϕ yθ, permanezcan constantes con el tiempo, es decir:

q = q = 0, con q = ϕ, θ.

Imponiendo esta condicion, las ecuaciones de equilibrio obtenidas son:

− sin ϕ · cos ϕ− ν · cos ϕ · cos θ + µ2 · sin ϕ + λ · ν · cos ϕ · sin θ = 0 (2.14)

ν · sin θ + λ · sin ϕ + λ · ν · cos θ = 0 (2.15)


Multiplicando la ecuacion (2.14) por λ y dividiendo por cos ϕ, y restandoel resultado a la ecuacion (2.15), obtenemos lo siguiente:

µ2 · λ · tan ϕ = −ν · (λ2 + 1) · sin θ (2.16)

−λ · sin ϕ = ν (sin θ + λ · cos θ) (2.17)

En la primera ecuacion obtenida, queda reflejada la relacion entre lossignos de ϕ y θ, puesto que los parametros que aparecen en dicha ecuaciontienen bien definido su signo. Ası, podemos deducir lo siguiente:

Si 0 < ϕ <π

2=⇒ −π < θ < 0

Siπ

2< ϕ < π =⇒ 0 < θ < π

Basandonos en este criterio de signos y en el cumplimiento del equilibrioentre las fuerzas que actuan sobre la masa m, resolveremos graficamente losdistintos cuadrantes de nuestro sistema donde podrıan existir soluciones, yaquellos en los que nunca existiran.

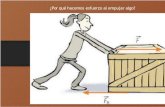
ωt

Y

T

Fc

mg

ϕ

Z

Y

Fc

T

θ

FrX

Figura 2.2: Primera clase de equilibrio.


En la Figura 2.2, podemos ver el primer tipo de equilibrio que existe para0 < ϕ < π

2y, como consecuencia de la ecuacion (2.16), para −π < θ < 0.

La tension de la barra (T ), provoca sobre este una traccion que en el planovertical se ve compensada por la fuerza centrıfuga Fc y el peso mg, y en elplano horizontal por la Fc y el rozamiento Fr. Este es el tipo de equilibrioclasico del pendulo esferico sometido a rotacion, y siempre es estable.

El segundo tipo de equilibrio es el de la Figura 2.3, y se denomina penduloesferico invertido. En este equilibrio, π

2< ϕ < π y 0 < θ < π, y es el valor del

angulo ϕ el que le hace tomar una posicion que genera un potencial convexoque le hace ser siempre inestable.

ωt

ϕ

θ

T

Fc

mg

T

Fc

Fr

X

Z

Y

Y

Figura 2.3: Segunda clase de equilibrio.

Por ultimo. presentamos en la Figura 2.4, la tercera clase de equilibrio. Enella 0 < ϕ < π

2y −π < θ < 0. Este tipo de equilibrio solo se puede dar para

determinadas relaciones de las longitudes de las barras b y `, concretamentey refiriendonos al parametro adimensional ν, para valores de ν menores que


uno, ya que la masa m tiene que pasar por el centro de rotacion, y ası lafuerza centrıfuga poder equilibrar a la tension de compresion del hilo.

Este tipo de equilibrio es el mas desconocido y, ademas, el mas interesante,ya que es el menos previsible en cuanto a estabilidad e inestabilidad y, porlo tanto, sera el objeto de estudio de el presente proyecto.

ωt

XFc

Z

Y

Y

ϕ

−θ

T

Fc

mg

TFr

Figura 2.4: Tercera clase de equilibrio.

Como hemos podido observar en las figuras que se han descrito anterior-mente, tan solo existen tres regiones donde es posible el equilibrio, ya queson las unicas en las que se cumple equilibrio en la proyeccion vertical (entrela tension T , la fuerza centrıfuga provocada por el giro Fc y el peso de lamasa que se encuentra en el extremo del pendulo mg) y en la proyeccionhorizontal (entre la tension T , la fuerza centrıfuga provocada por el giro Fcy la fuerza de rozamiento entre la masa m y el aire). Esto no quiere decir que


solo pueda haber tres equilibrios como mucho para unos parametros fijados,ya que en cada una de las zonas anteriores podrıa haber mas de uno, sino queen cualquier otra region es imposible la existencia de un punto de equilibrio.

Una vez realizado este pequeno estudio grafico, haremos un seguimientoanalıtico mas profundo de las dos ecuaciones de equilibrio obtenidas ante-riormente.

Para ello, manipularemos las ecuaciones (2.16) y (2.17) de la siguientemanera:

Elevamos la ecuacion (2.17) al cuadrado y escribimos el sin2 ϕ en fun-cion de la tan2 ϕ.

λ2 · tan2 ϕ

1 + tan2 ϕ= ν2 · [λ2 +

(1− λ2

) · sin2 θ + λ · sin (2θ)]

Elevamos la ecuacion (2.16) al cuadrado y despejamos la tan2 ϕ enfuncion de θ.

tan2 ϕ =ν2 · (λ2 + 1)

2 ·µ4λ2

· sin2 θ

Sustituimos la tan2 ϕ de la segunda expresion en la primera, obteniendouna ecuacion en funcion de θ unicamente.

λ2 · (λ2 + 1) · sin2 θ

µ4λ2 + ν2 · (λ2 + 1) · sin2 θ= λ2 +

(1− λ2

) · sin2 θ + λ · sin (2θ)

Hacemos el cambio de variable s = tan θ, obteniendo. . .

λ2 · (λ2 + 1) · s2

1 + s2

µ4λ2 + ν2 · (λ2 + 1) · s2

1 + s2

= λ2 +(1− λ2

) · s2

1 + s2+ λ · 2s

1 + s2

Desarrollamos el polinomio en s.

0=s4 · (λ4 + λ2 − ν2λ2 − ν2) + s3 · (−2µ4ν3 − 2ν2λ− 2ν2λ3)

+s2 · (λ4 + λ2 − 2µ4λ4 − ν2λ4 − ν2λ2 − µ4 − µ2λ2 + µ4λ4)

+s · (−2− µ4λ3)− µ4λ4

Hacemos el cambio de variable s = k · λ para quedarnos con una unicavariable independiente k, y ademas truncaremos el desarrollo en los


terminos de cuarto orden, quedandonos ası con los mas significativos.La ecuacion en k obtenida es la siguiente:

(k + 1)2 =k2

ν2k2 + µ4(2.18)

Evidentemente, la ecuacion obtenida no representa la solucion analıticadel problema, puesto que el cambio s = k ·λ ha sido elegido para obtener unaecuacion con una sola variable independiente. Sin embargo, esta ecuacion nosda una idea cualitativa de las posibles soluciones de equilibrio para el casoen el que 0 < λ << 1 (donde tiene sentido despreciar terminos de orden en λmayores que cuatro), ası como del comportamiento de las mismas en funcionde nuestros parametros mas significativos µ y ν.

(0,0) k−k

ν

µ = cte

Figura 2.5: Parametro ν variando.

Para comprender el significado de la ecuacion a la que hemos llegado,representaremos graficamente cada uno de los terminos de la igualdad y es-tudiaremos los posibles cortes en funcion de nuestras variables µ y ν.

El primer miembro de la ecuacion es (k + 1)2, que representa una parabolaconcava que tiene su vertice en el punto de coordenadas (−1, 0), y que ademases independiente de los parametros µ y ν.

El segundo miembro depende de ambos parametros µ y ν. Para estudiardicha dependencia de la funcion k2

ν2k2+µ4 con los parametros, veremos dosgraficas, una con ν variando y µ constante y otra de forma contraria.


En primer lugar, mostraremos la influencia del parametro ν en la funcion(Figura 2.5). Dicha funcion esta limitada superiormente por una asıntota ho-rizontal de valor 1

ν2 , ya que lımk→∞

k2

ν2k2+µ4 = 1ν2 , lo cual nos indica que mientras

mayor sea ν mas baja estara la asıntota.En segundo lugar, en la Figura 2.6, podemos ver la influencia del parame-

tro µ en la funcion, permaneciendo ν constante. Conforme el parametro µ vadisminuyendo, el grafico de la funcion se va haciendo mas amplio en el eje deabscisas y viceversa.

(0,0)

ν = cte

µ

−k k

Figura 2.6: Parametro µ variando.

Una vez mostrados como influyen los parametros µ y ν en el segundomiembro de la ecuacion (2.18), mostraremos una grafica de ambos miembrosde la ecuacion con el objetivo de estudiar los distintos puntos de cortes enfuncion de los parametros antes establecidos (Figura 2.7).

De las tres curvas que aparecen en el grafico, las dos nombradas CURVA 1y CURVA 2 corresponden al segundo miembro de la ecuacion (2.18) condistintos valores de los parametros µ y ν, mientras que la etiquetada comoPARABOLA, corresponde al primer miembro de la misma ecuacion.

Como podemos observar, la CURVA 1 corta a la PARABOLA en cuatropuntos, mientras que la CURVA 2 lo hace solo en dos. Ello se debe a que laprimera, tiene un parametro µ mas pequeno que la segunda, lo cual, comovimos en la Figura 2.6, provoca que sea menos abierta y le da la posibilidadde cortar a la parabola. Sin embargo, el parametro ν tambien cumple su


papel, ya que si la asıntota estuviera demasiado baja no serıa posible dichocorte.

(−1,0) (0,0) k−k

CURVA 1

PA

RÁ

BO

LA

CURVA 2

Figura 2.7: Solucion de la ecuacion aproximada..

La Figura 2.7, nos da la oportunidad de profundizar algo mas en el he-cho de que existan dos o cuatro soluciones. Si volvemos a las Figuras 2.2,2.3 y 2.4, recordaremos que de las tres regiones posibles donde pueden existirequilibrios, solo la primera y la segunda podrıan existir siempre independien-temente del valor de la relacion entre los brazos ν, ya que la tercera requerirıaque dicho parametro tomara valores inferiores a la unidad para que el brazode longitud ` fuera mayor que el de longitud b. Debido a ello, concluimosdiciendo que las dos soluciones que figuran tanto en la CURVA 1 como en laCURVA 2, reflejan las soluciones de equilibrio del pendulo correspondientes alas dos primeras clases de equilibrio, mientras que las dos soluciones restantesde la primera curva, son las correspondientes a dos equilibrios de la terceraregion que existiran para unos rangos de valores concretos de los parame-tros µ y ν. A su vez, tambien podemos deducir, que nunca existiran los dosultimos cortes en aquellas curvas en las que el valor de ν sea inferior a launidad, es decir, aquellas cuya asıntota horizontal este por debajo de uno, yque existira una curva crıtica en la que habra tres puntos de corte, y corres-pondera exactamente al valor ν = 1 siempre que µ sea lo suficientementepequeno.

Capıtulo 3

Continuacion numerica deequilibrios.

En el capıtulo anterior, se obtuvieron las ecuaciones diferenciales de mo-vimiento de nuestro modelo, y de forma analıtica y grafica obtuvimos unaserie de resultados que nos hacıan ver los posibles equilibrios y su situacionaproximada.

Nuestro objetivo en este capıtulo, sera obtener mediante el programade continuacion numerica AUTO2000, las curvas que representan todos losequilibrios del sistema segun vayan variando los parametros establecidos enel capıtulo anterior, ası como las posibles orbitas periodicas procedentes dealgunos de dichos equilibrios.

3.1. Introduccion.

Para realizar la continuacion numerica de una funcion escalar o vectorial,lo primero que debemos saber es que el numero de incognitas solo puede seruno mas que el de ecuaciones, es decir, que solo podemos tener un parametrode continuacion. Esto se debe, a que la continuacion numerica, se encarga deevaluar nuestra funcion para cada valor del parametro, y ası se va obteniendouna serie de puntos que definen nuestros equilibrios u orbitas periodicas,segun sea el caso. Una excepcion al caso anterior, son los puntos especialescomo puntos lımite, puntos de bifurcacion, puntos de Hopf, etc, ya que cuandose continua uno de estos puntos, implıcitamente se impone una ecuacion mas(un autovalor cero en caso de puntos lımite, por ejemplo), lo cual nos permitevariar dos parametros en lugar de uno solo.

En el caso concreto de nuestro sistema, las ecuaciones que rigen el mo-vimiento del pendulo son dos ecuaciones diferenciales de segundo orden con

18

CAPITULO 3. CONTINUACION NUMERICA DE EQUILIBRIOS. 19

cinco variables (ϕ, θ, µ, ν y λ):

0=ϕ− sin ϕ · cos ϕ ·(1 + θ

)2

− ν · cos ϕ · cos θ + µ2 · sin ϕ

+λ · ϕ + λ · ν · cos ϕ · sin θ

0=θ · sin ϕ + 2 · cos θ ·(1 + θ

)· ϕ + ν · sin θ + λ · sin ϕ ·

(1 + θ

)

+λ · ν · cos θ

Estas dos ecuaciones con derivadas de segundo orden, se pueden transfor-mar en cuatro ecuaciones en derivadas primeras introduciendo dos variables:

ψ = ϕ

Θ = θ + 1

Realizando este cambio de variable y despejando las derivadas primerasde las cuatro incognitas, obtenemos las ecuaciones que emplearemos en lacontinuacion numerica.

ϕ = ψ (3.1)

θ = Θ− 1 (3.2)

ψ=Θ2 · sin ϕ · cos ϕ + ν · cos ϕ · cos θ − µ2 · sin ϕ

−λ · ψ − λ · ν · cos ϕ · sin θ(3.3)

Θ=−2 · cos θ

sin ϕ·Θ · ψ − ν · sin θ

sin ϕ− λ ·Θ− λ · ν · cos θ

sin ϕ(3.4)

Segun la regla establecida al principio de este apartado, solo podemos te-ner un parametro de continuacion, con lo cual, fijaremos ν y λ y emplearemoscomo parametro libre la relacion de frecuencias µ.


3.2. Funcionamiento de AUTO2000.

AUTO2000 es el software de continuacion numerica que manejaremos enel presente proyecto. En este apartado explicaremos basicamente, los ficherosque hay que introducirle a AUTO para su funcionamiento, las ordenes nece-sarias para que funcione y los ficheros que genera despues de la continuacion.Posteriormente, en los apartados sucesivos, iremos particularizando todo ellopara nuestro sistema.

El funcionamiento de AUTO se basa en dos tipos de archivo:

Fichero xxx.c contiene varias subrutinas en C, en las que se introducenlas ecuaciones diferenciales del movimiento, ası como las condicionesiniciales tales como un punto de equilibrio, las condiciones de contorno,etc. . .

Fichero c.xxx en el que se refleja la dimension del sistema, los parametrosa continuar, las tolerancias admisibles, el numero de iteraciones, etc. . .

Vamos a mostrar un ejemplo de cada uno de estos ficheros y daremosunas nociones basicas de los parametros que hay que introducirles.

Para empezar, mostraremos un fichero tipo xxx.c a modo de ejemplo yveremos como funciona.

#include "auto_f2c.h"

int func (integer ndim, const doublereal *u, const integer *icp,

const doublereal *par, integer ijac,

doublereal *f, doublereal *dfdu, doublereal *dfdp) {

doublereal fi,teta,psi,Teta,mu,lambda,nu;

fi = u[0];

teta = u[1];

psi = u[2];

Teta = u[3];

mu=par[0];

lambda=par[1];

nu=par[2];

f[0]= psi;

f[1]= Teta-1;

f[2] = Teta*Teta*sin(fi)*cos(fi)+nu*cos(fi)*cos(teta)


-mu*mu*sin(fi)-lambda*psi-lambda*nu*cos(fi)*sin(teta);

f[3] = -2*cos(teta)*Teta*psi/sin(fi)-nu*sin(teta)/sin(fi)

-lambda*Teta-lambda*nu*cos(teta)/sin(fi);

return 0;

}

int stpnt (integer ndim, doublereal t,

doublereal *u, doublereal *par) {

/* Parametros iniciales */

par[0] = (doublereal)0.0;



/* Solucion inicial */

u[0] = (doublereal)1.57;

u[1] = (doublereal)-0.481;

u[2] = (doublereal)0.;

u[3] = (doublereal)1.;

return 0;

}

Aunque el fichero no esta completo, mostramos la parte de el que utiliza-remos, lo cual no implica que a la hora de ejecutarlo con el programa AUTOnos olvidemos del resto de funciones que son totalmente necesarias.

En este fichero, podemos distinguir dos funciones:

func es la encargada de pasar a AUTO las ecuaciones diferenciales y dedefinir las variables independientes y los parametros.

stpnt es la funcion que AUTO emplea cuando se le indica que comience lacontinuacion a partir de una solucion inicial.

Como hemos dicho antes, ademas de las funciones func y stpnt, existencuatro mas (bcnd, icnd, fopt y pvls) que se utilizan cuando se definencondiciones de contorno, condiciones de integracion, etc. . . y que, aunque nocontengan nada, deben incluirse en este fichero.

Este fichero, solo es necesario modificarlo si se quiere partir de otra solu-cion inicial, para lo cual tendrıamos que variar unicamente la funcion stpnt.En cualquier otro caso, al permanecer las ecuaciones diferenciales inaltera-bles, no serıa necesaria su modificacion.


Una vez mostrado un fichero tipo xxx.c, explicaremos el otro ficheronecesario para trabajar con AUTO, el c.xxx.

Este fichero sera el que de a AUTO las condiciones en las que debe realizarla continuacion de las ecuaciones definidas en xxx.c. Veamos un ejemplo:

4 1 0 1 NDIM,IPS,IRS,ILP

3 0 2 1 NICP,(ICP(I),I=1 NICP)

100 4 3 1 1 0 0 0 NTST,NCOL,IAD,ISP,ISW,IPLT,NBC,NINT

180 0 100 0 100 NMX,RL0,RL1,A0,A1

180 5 2 8 7 5 0 NPR,MXBF,IID,ITMX,ITNW,NWTN,JAC

1e-7 1e-7 1e-5 EPSL,EPSU,EPSS

0.001 0.001 0.01 1 DS,DSMIN,DSMAX,IADS

0 NTHL,(/,I,THL(I)),I=1,NTHL)

0 NTHU,(/,I,THU(I)),I=1,NTHU)

0 NUZR,(/,I,PAR(I)),I=1,NUZR)

Vamos a explicar los parametros mas importantes de este fichero:

NDIM indica la dimension del sistema de ecuaciones. En el caso quenos aborda tenemos cuatro ecuaciones en derivadas primeras.

IPS define el tipo de problema. Nosotros nos moveremos entre dos desus valores:

• IPS=1 Soluciones estacionarias de ecuaciones diferenciales ordi-narias con deteccion de bifurcaciones de Hopf.

• IPS=2 Para continuacion de soluciones periodicas.

IRS define la etiqueta de la solucion donde la continuacion comenzara.Si su valor es cero, como en este caso, el programa tomara como solucioninicial la indicada en la funcion stpnt.

ILP tiene dos valores posibles:

• ILP=0 No detecta los posibles pliegues de la continuacion.

• ILP=1 Detecta los pliegues de la continuacion (puntos LP). Es elvalor recomendado.

NICP indica el numero de parametros que tiene nuestro sistema. Ennuestro caso son µ, λ y ν, y por ello le hemos asignado a esta variableel valor 3. En realidad, el numero de parametros esta definido en elarchivo xxx.c con un vector llamado PAR[], y en el NICP lo unico queindicaremos es cuantos de ellos queremos que aparezcan por pantallaal ejecutar AUTO.


ICP depende del valor que hallamos asignado a NICP. Deberemosindicar que parametros seran los que apareceran en la continuacion ysegun el orden, cual sera el parametro de continuacion principal y cualel secundario. En nuestro caso, hemos indicado un valor de NICP=3,luego hemos elegido los tres parametros de continuacion; PAR[0] enprimer lugar (µ) como parametro de continuacion principal, PAR[2] (ν)como segundo parametro de continuacion, y PAR[1] (λ) como tercerparametro. Como el parametro λ es el mismo a lo largo de todo elproyecto, podrıamos indicarle a AUTO que no lo mostrara por pantalla,para lo cual, lo unico que tendrıamos que hacer es darle a NICP el valor2, y al vector ICP los valores 0 y 2 correspondientes a µ y ν.

ISP es el parametro que controla la deteccion de puntos de bifurca-cion (BP), puntos de bifurcacion de doble perıodo (PD), etc. Nosotrosemplearemos dos valores de esta variable:

• ISP=1 Este valor detecta puntos de bifurcacion (HB) para solu-ciones que no sean periodicas, y no detecta puntos de bifurcacionde doble perıodo (PD).

• ISP=2 Este valor detecta todos los puntos especiales y es el queemplearemos cuando trabajemos con orbitas periodicas.

ISW indica el tipo de continuacion que realizaremos. Nosotros emplea-remos tres valores:

• ISW=1 Se utiliza para continuar equilibrios con un solo parametroy para trazar una orbita periodica a partir de un punto de Hopf.

• ISW=2 Se utiliza para continuar puntos lımite (PL) y puntos deHopf (HB), ya que al anadirse implıcitamente una ecuacion enestos puntos, se nos permite variar un segundo parametro.

• ISW=−1 Se utiliza en orbitas periodicas para continuar puntos debifurcacion (BP) y puntos de bifurcacion de doble perıodo (PD).

NMX indica el numero maximo de iteraciones que le vamos a permitira la continuacion.

RL0, RL1 indican el valor mınimo y maximo, respectivamente, quepuede tomar el parametro de continuacion principal, en este caso µ.

NPR Si su valor es inferior a NMX, entonces se mostraran por pantallalos resultados cada NPR iteraciones. Si su valor es igual a NMX, solose mostraran por pantalla los puntos especiales encontrados (dichospuntos tambien apareceran en el caso anterior).


DS indica el tamano de paso normal entre dos puntos de la mismarama. Ademas, un cambio de signo, provoca que la continuacion serealice en sentido contrario.

DSMIN, DSMAX indican en valor absoluto los tamanos de pasomınimo y maximo admisibles entre dos puntos de l misma rama.

Una vez introducidos los ficheros, nos situamos en el directorio donde seencuentran y desde consola ejecutamos el programa escribiendo auto (escri-bir en minusculas). El resultado sera algo parecido a la Figura 3.1.

Figura 3.1: Ejecucion de AUTO.

Dentro del programa, tenemos que cargar los ficheros xxx.c y c.xxx, locual se puede hacer de dos formas:

Cargando primero el fichero de ecuaciones y luego el fichero de cons-tantes:

AUTO>ld(’xxx’)

AUTO>r(c=’xxx’)

Cargando los dos ficheros a la vez:

AUTO>r(e=’xxx’,c=’xxx’)

Una vez ejecutadas estas ordenes, el programa nos devuelve tres ficherosfort con las extensiones 7, 8 y 9:

fort.7 contiene los valores de los parametros de continuacion para cada unade las iteraciones que nos permitiran dibujar el diagrama de bifurcacion.


fort.8 contiene informacion mas extensa de cada una de las orbitas etique-tadas.

fort.9 contiene mensajes de diagnostico, convergencia de las soluciones, au-tovalores, etc. . .

Sera por medio de estos tres ficheros que podamos representar grafica-mente la continuacion y podamos obtener los autovalores.

3.3. Continuacion numerica de las ecuaciones

de nuestro modelo.

En este apartado, iremos mostrando paso por paso los resultados delacontinuacion numerica aplicada a las ecuaciones diferenciales de movimien-to de nuestro sistema. A su vez, iremos mostrando los distintos ficheros deAUTO que emplearemos y los resultados que nos va dando este software decontinuacion numerica.

3.3.1. Calculo de equilibrios

Antes de calcular los puntos de equilibrio que daran inicio a la conti-nuacion numerica, conviene senalar que como solo podemos disponer de unparametro de continuacion o dos en algunos casos (continuacion de puntos es-peciales), vamos a fijar el valor del coeficiente adimensional de rozamiento enλ = 0,2 y sera el que utilicemos a lo largo de todo el proyecto. Ademas, comoparametro principal de continuacion, manejaremos la relacion de frecuencias

µ =

√g`

ωy, como parametro secundario, la relacion de brazos ν = b

`.

Como vimos en el apartado 2.3, solo existen tres zonas donde se puedendar los equilibrios, ası que emplearemos Matlab para hallar al menos un puntode equilibrio en cada una de estas zonas y comenzaremos la continuacionnumerica a partir de dichos puntos.

La primera clase de equilibrio que estudiaremos es la correspondiente ala Figura 3.2, e implica unos valores de ϕ comprendidos en

[0, π

2

], y unos

valores de θ pertenecientes al intervalo[−π

2, 0

].

Para buscar un punto inicial de equilibrio de este tipo, hemos partido delos valores

µ=0

ν=0,7

λ=0,2


Figura 3.2: Primera clase de equilibrio.

dando como resultado las variables independientes:

ϕ=1,57 rad

θ=−0,481 rad

ψ=0rad

seg

Θ=1rad

seg

La segunda clase de equilibrio que estudiaremos es la correspondiente ala Figura 3.3, e implica unos valores de ϕ comprendidos en

[π2, π

], y unos

valores de θ pertenecientes al intervalo[

π2, π

].


µ=0

ν=0,7

λ=0,2




ϕ=2,366 rad

θ=3,141 rad

ψ=0rad

seg

Θ=1rad

seg

Por ultimo, la tercera clase de equilibrio que estudiaremos es la correspon-diente a la Figura 3.4, e implica unos valores de ϕ comprendidos en

[0, π

2

], y

unos valores de θ pertenecientes al intervalo[π, 3π

2

].


µ=0

ν=0,7

λ=0,2




ϕ=0,775 rad

θ=3,141 rad

ψ=0rad

seg

Θ=1rad

seg

Es necesario mencionar que el valor del parametro µ escogido implica queestamos dando una frecuencia de giro infinita, y debido a ello, los valores dela variable θ estan tan cercanos a π, en el caso de los equilibrios de tipo 1y 3, o a 0 en el caso de los equilibrios de tipo 2. Por el mismo motivo, losvalores de ϕ tambien son tan extremos.

3.3.2. Continuacion de los equilibrios.

En este apartado, comenzaremos a utilizar AUTO para continuar los equi-librios hallados anteriormente.

En primer lugar, creamos tres ficheros llamados equi1.c, equi2.c y equi3.c,los cuales tienen la misma funcion func, ya que todos tienen las mismas ecua-ciones, y distinta funcion stpnt, ya que cada uno de ellos corresponde a unode los equilibrios y tienen distintas condiciones iniciales (concretamente lashalladas con MATLAB en el apartado anterior).


Del mismo modo, creamos ahora tres ficheros llamados c.equi1, c.equi2y c.equi3, los cuales contienen los parametros de continuacion de AUTO.Estos tres ficheros son iguales, salvo el numero de iteraciones que cambia enalguno de los equilibrios. Mostraremos el del equilibrio 1 representando a lostres:


3 0 2 1 NICP,(ICP(I),I=1 NICP)


180 0 100 0 100 NMX,RL0,RL1,A0,A1







Los parametros mas destacables de este fichero son:

IRS=0 Partimos del equilibrio que nos da la funcion stpnt.

ISW=1 Continuamos un solo parametro (en este caso µ).

NMX=180 Haremos un maximo de 180 iteraciones.

NPR=180 Solo se mostraran las etiquetas de los puntos especiales.

Una vez creados los seis archivos mencionados, dos por cada tipo de equi-librio, ejecutaremos AUTO y veremos los resultados obtenidos por pantalla.Para ello, abriremos la consola, e iremos al directorio donde hemos creadolos seis ficheros. Una vez allı teclearemos lo siguiente:

auto

AUTO>ld(’equi1’)

AUTO>r(c=’equi1’)

La salida por consola se muestra en la Figura 3.5. En ella podemos obser-var como AUTO nos da el valor de los parametros para las iteraciones 1 y 180en este caso, ya que no ha existido ningun punto especial entre ellos. Si en elarchivo c.equi1 le hubieramos dado a la constante NPR un valor inferior a180, podrıamos ver mas etiquetas en puntos intermedios y ademas la evolu-cion de los distintos parametros y variables independientes. Sin embargo, nolo hacemos de esta manera porque AUTO es capaz de representarnos grafica-mente la solucion de la continuacion, donde se ve el resultado mas claramente.


Ademas podemos ver como AUTO nos etiqueta los puntos representados conunos determinados numeros que, como veremos posteriormente, nos serviranpara hacer referencia a dichos puntos.

Figura 3.5: Ejecucion del fichero “equi1”.

Para guardar los cambios, utilizamos el siguiente comando:

AUTO>sv(’equi1’)

Al utilizar el comando save o sv, se generan los siguientes ficheros:

b.equi1 que contiene los valores de los parametros de continuacion paracada una de las iteraciones, y nos permitira dibujar el diagrama debifurcacion.

s.equi1 que contiene informacion mas extensa de cada una de las iteracionesetiquetadas.

d.equi que contiene mensajes de diagnostico, convergencia de soluciones,autovalores, etc.

Para representar graficamente la solucion recurrimos al comando plot o pl.Si lo llamamos sin pasarle ningun argumento, representara lo que encuentreen los ficheros fort7, fort8 y fort9. Sin embargo, si queremos que nos representela grafica de unos determinados ficheros b.xxx, s.xxx y d.xxx, entonces letendremos que pasar como parametro ‘xxx’. Mostraremos como ejemplo loque tendrıamos que escribir por consola para representar la grafica de ‘equi1’:

AUTO>pl(’equi1’)


Debido a que el entorno grafico de AUTO no es demasiado preciso, he-mos optado por representar las graficas de este documento con MATLABimportando los datos que genera AUTO en el fichero ‘b.xxx’.

Una vez explicado los comandos principales de AUTO, vamos a repre-sentar la continuacion numerica hecha en el fichero ‘equi1’ que, recordemos,tiene un valor de ν constante e igual a 0.7. En dicha representacion, mostra-remos el angulo ϕ(µ) frente al parametro principal de continuacion µ en laFigura 3.6, y el angulo θ(µ) frente al mismo parametro en la Figura 3.7.

0 0.2 0.4 0.6 0.8 1 1.2 1.40.4

0.6

0.8

1

1.2

1.4

1.6

1.8

µ

ϕ

Figura 3.6: ϕ frente a µ de un equilibrio tipo 1 con ν = 0,7.

En la Figura 3.6, podemos observar como conforme aumentamos µ (dis-minuimos la velocidad de giro) el angulo ϕ va disminuyendo. Este resultadoes perfectamente logico, ya que si observamos la Figura 3.2, nos damos cuentade que el pendulo se ira acercando a la vertical cuando la velocidad disminuyey se ira alejando de la misma cuando la velocidad aumenta. Concretamente,para µ = 0 (velocidad infinita), alcanzara el maximo valor del angulo ϕ (casi90 grados), ya que la fuerza centrıfuga llegara a ser maxima para el valor deν que estamos estudiando.


0 0.2 0.4 0.6 0.8 1 1.2 1.4−0.5

−0.48

−0.46

−0.44

−0.42

−0.4

−0.38

−0.36

−0.34

µ

θ

Figura 3.7: θ frente a µ de un equilibrio tipo 1 con ν=0.7.

Veamos ahora en la Figura 3.7 como afecta al angulo θ la velocidad degiro. Para valores de µ muy cercanos a cero, el retraso del pendulo alcanzavalores muy altos, del orden de los−27 grados o−0,47rad, ya que la velocidades casi infinita. Sin embargo, conforme vamos disminuyendo la velocidad, esdecir, aumentando el parametro µ, el retraso del pendulo se va haciendo cadavez menor como era de esperar, ya que en el caso ideal en el que no existeel rozamiento, el pendulo permanece en el mismo plano vertical que la barrade longitud b, lo que indicarıa un angulo θ de valor cero.

Aunque este tipo de equilibrios correspondientes a la Figura 3.2 esta yamuy estudiado en la mecanica y se sabe que siempre es estable, nosotrosvamos a estudiar como evolucionan sus autovalores, y comprobaremos que,efectivamente, siempre se encuentran en la parte negativa del espectro, lo cualindica estabilidad. Concretamente, para nuestro fichero ´equi1’, le pediremoslos autovalores a AUTO mediante la orden ev, eg o eigenvalue de la siguienteforma:

AUTO>ev(’equi1’)

Si observamos la evolucion de los cuatro autovalores, nos daremos cuentade que forman dos pares conjugados que se mueven siempre con partes reales


negativas, lo cual indica, como hemos dicho anteriormente, que siempre esestable para cualquier rango de velocidades. En la Figura 3.8 mostramos unaposicion representativa del espectro de los cuatro autovalores.

Im

Re

Figura 3.8: Espectro de autovalores para el fichero ‘c.equi1’.

Una vez realizado el estudio de los que hemos llamado equilibrios de tipo1 para un valor de ν = 0,7, correspondiente a el fichero ‘c.equi1’, haremos elmismo razonamiento con el siguiente tipo de equilibrio, al que hemos llamadoequilibrio de tipo 2 y al cual, en notacion de AUTO, lo designamos con elfichero ‘c.equi2’.

Los equilibrios de tipo 2, vienen representados de forma generica en laFigura 3.3. Vamos a pedirle a AUTO que nos continue el punto de equilibriocorrespondiente a µ = 0 para el mismo valor de ν que en el caso anterior.Para ello, le daremos los siguientes comandos:


AUTO>r(c=’equi2’)

En este caso, el fichero ‘c.equi2’ es exactamente igual que el usado ante-riormente, ya que los parametros de continuacion son los mismos, y lo unicoque cambia de un equilibrio a otro es el equilibrio inicial, reflejado en elfichero ‘equi2.c’.

Al igual que en el equilibrio anterior, exportamos a MATLAB los datosobtenidos y hacemos dos representaciones graficas, una correspondiente alangulo ϕ frente al parametro µ (Figura 3.9), y otra al angulo θ frente almismo parametro (Figura 3.10).


0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.82.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

3

µ

ϕ


En las Figuras 3.9 y 3.10 podemos observar como al aumentar la frecuen-cia de giro (disminuir µ), el angulo ϕ disminuye, separandose el pendulo dela vertical, y el angulo θ aumenta, disminuyendo el pendulo el retraso. Estecomportamiento quizas no es el que se espera intuitivamente, ya que parecelogico que al aumentar la velocidad, el pendulo se retrase y se acerque a lavertical.


0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.82.98

3

3.02

3.04

3.06

3.08

3.1

3.12

3.14

3.16

3.18

µ

θ


Im

Re

Figura 3.11: Espectro de autovalores para el fichero ‘c.equi2’.

Veamos ahora el comportamiento de los autovalores para los equilibriosde tipo 2 con ν = 0,7. Para ello, teclearemos en AUTO lo siguiente:

AUTO>ev(’equi2’)


Como era de esperar, el espectro de autovalores nos da siempre inestabi-lidad, ya que si observamos la Figura 3.11, podemos ver como siempre existeuna pareja de autovalores conjugados en la parte real negativa, y otra pare-ja en la parte real positiva que es la que provoca la inestabilidad. Tambienpodıamos haber llegado a esta conclusion a partir de la curva de potencialde este tipo de equilibrios, la cual siempre es concava, desvelando dicha ines-tabilidad.

Por ultimo, continuaremos el tipo de equilibrio 3 que, a priori, es el masinteresante y desconocido de todos. Una posicion aproximada del pendulo enesta clase de equilibrio la vimos en la Figura 3.4. Debemos tener en cuentaque esta posicion, solo se puede dar para una determinada relacion de brazos,concretamente para ν = b

`< 1, y es por este motivo por el que hemos tomado

el valor ν = 0,7 y no uno superior a la unidad, y ası puedan coexistir los trestipos de equilibrio.

Si ejecutamos la continuacion del equilibrio correspondiente al fichero‘equi3’, encontramos que AUTO nos da en un punto intermedio de la conti-nuacion una etiqueta LPque no habıamos visto anteriormente. Esta etiqueta,representa un Punto Lımite, el cual nos separa dos ramas de equilibrios dife-rentes, es decir, partiendo de un equilibrio y, continuandolo, hemos detectadoun segundo equilibrio.

−0.05 0 0.05 0.1 0.15 0.2 0.25 0.3 0.350.7

0.8

0.9

1

1.1

1.2

1.3

1.4

1.5

1.6

µ

ϕ

LP



−0.05 0 0.05 0.1 0.15 0.2 0.25 0.3 0.353.14

3.15

3.16

3.17

3.18

3.19

3.2

3.21

3.22

3.23

µ

θ

LP


En la Figura 3.12, vemos la representacion grafica del angulo ϕ frente alparametro µ. Hemos marcado el punto lımite que diferencia los dos equilibriosque coexisten. Uno de los equilibrios existe para valores mas bajos del anguloϕ, y conforme vamos disminuyendo la velocidad, se va separando mas de lavertical. El otro, tiene un angulo ϕ mayor, y ademas, conforme disminuimos lavelocidad, reacciona disminuyendo su angulo con la vertical. Ambos coincidenel punto lımite, el cual nos indica la menor velocidad para la que existe estetipo de equilibrio.

Tambien se ha representado el angulo θ frente al parametro µ. De nuevoaparece el punto lımite para distinguir los dos equilibrios, y podemos des-cubrir como siempre hay un equilibrio que se retrasa mas que el otro, con-cretamente, el de menor angulo ϕ tiene un angulo θ inferior para la mismafrecuencia de giro.

Veamos que sucede en el espectro de autovalores para ambos equilibrios.Para ello, partiremos del espectro en el punto lımite, ya que es un puntocomun a ambos equilibrios, y comprobaremos como se mueven los autova-lores. En la Figura 3.14 estan representados los autovalores en el LP. Estetipo de puntos, se caracteriza por tener uno de los autovalores en el cero,en este caso el representado con la etiqueta 1 en la grafica. Como podemosapreciar, tiene ademas un autovalor en el semieje real positivo, lo que lo hace


inestable.

Im

Re3 2 1 4

Figura 3.14: Autovalores en el punto lımite (LP).

Una vez que hemos visto como se comportan los autovalores en el LP,mostraremos en la Figura 3.15 hacia donde se mueven dichos autovalores alavanzar por cada una de las ramas. En esta figura, identificamos el diagramade la izquierda con el equilibrio inferior de la Figura 3.12 y el de la derechacon el superior.

Im

Re

Im

Re3 4

1

2

3 42 1

Figura 3.15: Espectro de autovalores a ambos lados del LP.

Hemos marcado en ambos espectros hacia donde se mueven los auto-valores en los dos equilibrios, y podemos observar como, en el primero, se


mantienen en el eje real y los cuatro se separan del eje imaginario, mientrasque en el segundo, dos de ellos se unen en el eje real y forman una parejaconjugada, y los otros dos, permanecen cada uno a ambos lados del eje imagi-nario. Dada la situacion de ambos equilibrios, podemos afirmar que ningunode ellos es estable.

Resumiendo este apartado, podemos decir que el unico equilibrio establepara el parametro ν con valor 0,7 es el que nosotros hemos denominadoequilibrio de tipo 1. En cuanto al equilibrio de tipo 2, hemos comprobadosu inestabilidad mediante sus autovalores y mediante la curva de potencial,y ya no se estudiara mas a lo largo de este documento. Por ultimo, en elequilibrio de tipo 3, para la relacion de brazos tratada, hemos comprobadoque coexisten dos tipos de equilibrios ambos inestables y que se encuentranconectados por un punto lımite, el cual sera nuestro objeto de estudio en elsiguiente apartado.

3.3.3. Continuacion del punto lımite (LP).

En este apartado, continuaremos el punto lımite que encontramos para elequilibrio de tipo 3, ya que este nos indicara en el espacio de bifurcaciones deν frente a µ para que relaciones de brazo y frecuencia de giro existen los dosequilibrios, y ademas sera capaz de mostrarnos la estabilidad de los mismos.En definitiva, continuar el LP variando los parametros µ y ν nos servira parasacar conclusiones sobre los equilibrios como las del apartado anterior, peroextendido a todo el campo de variacion de ν (en realidad solo abarcaremoslos valores de ν en los que se dan los equilibrios de tipo 3, es decir, los valoresde ν entre cero y uno).

Antes de pasar a la continuacion del punto lımite LP con AUTO, convienesenalar que de las dos ramas de equilibrios obtenidas en la Figura 3.12 o 3.13,el unico punto que podemos continuar en dos parametros es el LP, y esoes debido a que continuar un punto lımite, introduce implıcitamente unaecuacion extra, y es que uno de los autovalores sera siempre cero.

Otra forma mas basta de obtener la curva de LP que limita los equilibriosserıa realizar la tarea del apartado anterior para distintos valores de ν, y ası irtrazando dicha curva. Este metodo podrıa ser utilizado si no tuvieramos unprograma como AUTO capaz de continuar en dos parametros.

Sin mas preambulos, pasaremos a analizar el fichero ‘c.equi3.LP.0’, quesera el primer archivo de continuacion del LP. Con respecto a los anterioresficheros ‘c.xxx’, las diferencias vienen dadas por los siguientes parametros:

IRS=2 Nos permite continuar desde la etiqueta 2 (LP)del fichero que luego


escojamos desde la lınea de comandos y no desde un equilibrio inicialdado en la funcion stpnt.

ISW=2 Le indica al programa AUTO que continue en dos parametros, in-troduciendo este una ecuacion extra correspondiente, en el caso de unLP, a un autovalor cero.

Ademas de los cambios en los dos valores anteriores, hay que establecer elsegundo parametro a continuar en el vector ICP. En nuestro caso, tenemoscomo parametro principal de continuacion el PAR[0] (que representa a µ), ycomo parametro secundario el PAR[2] (que representa a ν).

Tambien hay que vigilar el signo que tiene la variable de entrada DS, yaque sera este el que establezca en que sentido nos moveremos a lo largo dela curva LP, si en sentido creciente de µ, o en sentido decreciente del mismo.Nosotros, concretamente, comenzaremos por disminuir el valor de µ, ası quele daremos a DS un signo negativo. Esto es arbitrario ya que, a priori, nosabemos hacia donde se encuentra el sentido decreciente del parametro.

Una vez analizadas las principales diferencias de ficheros, introducimos aAUTO las siguientes ordenes por consola:


AUTO>r(c=’equi3.LP.0’,s=’equi3’)

Con estas ordenes, lo que le estamos diciendo a AUTO es que partien-do de la solucion ‘equi3’, ejecutemos el fichero de constantes ‘equi3.LP.0’,basandonos siempre en las ecuaciones que hemos cargado anteriormente conel comando load. Esto tambien lo podrıamos hacer en una sola orden, queserıa la siguiente:

AUTO>r(e=’equi3’,c=’equi3.LP.0’,s=’equi3’)

En esta ocasion, en lugar de cargar primero el fichero de ecuaciones yluego el de constantes y la solucion, lo hemos hecho todo en un solo paso. Sinembargo, esto tiene un inconveniente, que solo carga el fichero de ecuacionespara el fichero de constantes especificado luego, en una proxima orden, ten-dremos que volver a llamar al fichero de ecuaciones, y si siempre es el mismo,como es nuestro caso, no aporta ningun beneficio.

Al ejecutar el fichero, obtenemos una curva en la que el parametro νaumenta hasta la unidad y el parametro µ disminuye hasta cero (Figura 3.16).Parece logico que la curva muera en ν = 1, ya que es imposible que existanequilibrios de tipo 3 para valores superiores.

A continuacion podrıamos cambiar el signo de DS en el fichero ‘c.equi3.LP.0’y trazar la curva en el otro sentido, sin embargo, lo que haremos sera partir


del punto de coordenadas ν = 1 y µ = 0 etiquetado como LAB 4 y continuarla curva entera de LP con el fichero ‘c.equi3.LP.1’.

0.7 0.75 0.8 0.85 0.9 0.95 10

0.05

0.1

0.15

0.2

0.25

0.3

0.35

ν

µ

Figura 3.16: Continuacion del LP para valores decrecientes de µ.

Nuestra forma de trabajar con AUTO a lo largo del proyecto sera crearun primer fichero terminado en cero que trace el inicio de la curva y, acontinuacion, crear otro terminado en uno que partiendo de la anterior, latrace entera etiquetando todos los puntos de la curva.

Veamos ahora los cambios introducidos en el nuevo fichero ‘c.equi3.LP.1’:

IRS=4 Nos permite continuar desde la etiqueta 4 que representa al ultimopunto de la curva LP (ν = 1 y µ = 0).

DS=+0,001 Le indica al programa AUTO que continue el parametro prin-cipal aumentandolo.

NPR=1 Etiquetamos todas las iteraciones que realice AUTO.

Corremos AUTO con los siguientes comandos:

AUTO>sv(’equi3.LP.0’)

AUTO>r(c=’equi3.LP.1’,s=’equi3.LP.0’)


AUTO>sv(’equi3.LP.1’)

AUTO>pl(’equi3.LP.1’)

Notese que lo primero que hemos hecho ha sido guardar el fichero anterior,ya que de otra forma no podrıamos partir de una etiqueta generada por el.Despues hemos ejecutado el nuevo fichero, lo hemos guardado y, por ultimolo hemos representado graficamente (ver Figura 3.17).

0 0.2 0.4 0.6 0.8 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1µ

ν

RAMA 1

RA

MA

2

LP C

B A

Figura 3.17: Curva completa de LP.

En la Figura 3.17, podemos observar como la propia curva de LP tiene unpunto lımite para el valor de µ mas alto, y ello genera dos ramas, diferenciadasen la grafica con distintos colores. Hay que tener en cuenta que un LP siempresepara dos equilibrios, luego si tenemos dos ramas de LP, estamos ante tresequilibrios, dos de ellos separados por la llamada “RAMA 1” en la grafica, yuno de los anteriores separado por la “RAMA 2” con un tercero.

Para ver que esta sucediendo en terminos de estabilidad a lo largo de cadauna de las ramas, vamos a observar el espectro de autovalores para cada unade ellas. Para ello, le pedimos a AUTO los autovalores del fichero ‘equi3.LP.1’de la siguiente forma:


AUTO>ev(’equi3.LP.1’)

0.1 0.15 0.2 0.25 0.3

0.6

0.65

0.7

0.75

0.8

0.85

0.9

C TB

HZ

µ

ν

Figura 3.18: Puntos destacados en la curva LP.

Al obtener los autovalores, podemos destacar tres puntos sobre los demas(ver Figura 3.18):

C: Punto de cuspide. Es el punto lımite que separa las dos ramasde LP.

TB: Doble cero. En este punto existen dos autovalores en el cero.

HZ: Hopf-Zero. Existe un par de autovalores conjugados en el ejeimaginario y otro autovalor en el cero.

En la Figura 3.19, hemos representado las posiciones aproximadas de losautovalores a lo largo de la rama 1. En dicha figura, se ha denominado comopunto A al de coordenadas ν = 1 y µ = 0.


TB C

Im

Re413

2

Im

Re1

Im

Re

PUNTO TB

Im

Re12

A TB

PUNTO C

2

3 4

3 4 13 2 4

Figura 3.19: Autovalores en la rama 1 del LP.

En primer lugar se toma el espectro de autovalores entre el punto A yel TB. En el podemos observar como los dos autovalores de la parte realnegativa y el de la parte real positiva, se van desplazando en busca del cero.Cuando llegan al punto TB el autovalor 2 ha alcanzado el cero, y el 3 y 4siguen en las partes reales negativa y positiva, respectivamente. Este doblecero, sera el inicio de la curva de Hopf que buscaremos en apartados posterio-res. Si seguimos avanzando por la rama, vemos como el autovalor 2 entra enla parte real positiva y se va acercando al 4, hasta llegar al punto de cuspideC. Como vemos, todos los equilibrios de la rama 1 son inestables, puesto que


siempre tienen al menos un autovalor positivo.

4

2

C HZ

Im

Re1

Im

Re413

PUNTO C

Im

Re1

2 3

2

4

Im

Re1

2

4

3 3

PUNTO TB

PUNTO HZ HZ B

Figura 3.20: Autovalores en la rama 2 del LP.

En la Figura 3.20, hemos representado las posiciones de los autovalores alo largo de la rama 2. En dicha figura, se ha denominado como punto B alde coordenadas ν = 0,196 y µ = 0. El espectro de autovalores comienza en elpunto C con dos autovalores en la parte real positiva, uno en el cero y otro enla parte real negativa. Cuando vamos bajando por la rama 2, lo que sucede esque los autovalores numerados 2 y 4, se acercan hasta formar uno doble, y apartir de ahı se convierten en una pareja de autovalores conjugados que se vaacercando al eje imaginario. Concretamente, cortan al dicho eje al llegar al


punto HZ, denominado ası por contener un cero y un Hopf (pareja de auto-valores conjugados en el eje imaginario). Sera a partir de este punto cuandola pareja de autovalores conjugados pase a la parte real negativa, no teniendotodos los puntos de equilibrio que restan hasta el punto B autovalores conparte real positiva.

La estabilidad de ese ultimo tramo de la rama 2, nos indica que alguno delos dos equilibrios que coexisten a ambos lados de la rama podrıa ser estable,ya que si el autovalor 1 se dirige hacia la parte real negativa tendrıamos 4autovalores negativos, es decir, estabilidad. Sin embargo, si el autovalor 1 semueve hacia la derecha, se acabarıa la inestabilidad. En apartados posterioresexplicaremos lo que sucede.

3.3.4. Continuacion del punto Hopf-Zero (HZ).

Al continuar la curva de LP, hicimos referencia a dos puntos particular-mente, el punto TB (doble cero), en el que nos encontrabamos dos autovaloresen el cero, y el punto HZ, que representa una situacion en la que se da unHopf (pareja de autovalores conjugados en el eje imaginario) y un cero.

En este apartado, trataremos de continuar el punto HZ, ya que su conti-nuacion nos dara una curva de equilibrios que tiene un par de autovalores enel eje imaginario, es decir, en esta curva se dara el paso de dos autovaloresde la parte real positiva a la parte real negativa, o viceversa.

Como el programa AUTO no ha sido capaz de detectarnos este puntocomo un Hopf, trazaremos sobre la Figura 3.17, una vertical que nos desvelealgun punto de Hopf a partir del cual podamos continuar la curva completa.Evidentemente, la vertical la tomaremos para un valor de ν proximo a nuestropunto HZ de coordenadas µ = 0,63 y ν = 0,179, y ademas pertenecientea la curva LP, ya que nos evitaremos tener que calcular un equilibrio conMATLAB si continuamos directamente uno de los dados anteriormente porel propio AUTO.

El punto escogido pertenece a la rama 1 de nuestra curva LP y tiene comocoordenada ν el valor 0,163, a la izquierda del HZ. En la Figura 3.21 podemosver el lugar aproximado de la vertical trazada. Para realizar la continuacion,haremos lo mismo que en el caso de la LP, y crearemos en primer lugarun fichero terminado en cero que nos continue la curva hasta uno de susextremos, en concreto hasta el que llega al eje µ = 0, y a partir de ese punto,trazaremos la curva completa.

Una vez hallado el punto que vamos a continuar, generamos un ficherollamado ‘c.vertical.3.0’ cuyos parametros mas significativos son los siguientes:


IRS=76 Define la etiqueta del punto correspondiente a la curva de LP quevamos a continuar.

ICP= 0 2 Define como primer parametro de continuacion a µ, y como se-gundo a ν.

ISW=1 Indica que la continuacion se hara en un parametro, en este casoen µ.

NPR=1 AUTO sacara por pantalla todas las iteraciones realizadas.

0.1 0.15 0.2 0.25 0.3

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

ν

µ

HZ

TB

ν =

0.16

3

Figura 3.21: Vertical trazada para ν = 0,163.

Creado el fichero ‘c.vertical.3.0’, ejecutamos AUTO con lo siguientes coman-dos:


AUTO>r(c=’vertical.3.0’,s=’equi3.LP.1.1’)

AUTO>sv(’vertical.3.0’)


AUTO, partiendo del LP, nos genera una serie de iteraciones sin destacarningun punto especial hasta que llega al eje µ = 0 con la etiqueta 153 y separa. Sera a partir de este punto, de donde partamos para recorrer la curvacompleta y encontrarnos con los tres equilibrios, ya que para este valor delparametro ν, cortaremos a las dos ramas de la curva LP.

Generamos ahora el fichero ‘c.vertical.3.1’, que sera exactamente igual alanterior salvo en el parametro IRS, que ahora tomara el valor 153 corres-pondiente a la etiqueta del punto que vamos a continuar.

En AUTO escribirıamos lo siguiente:

AUTO>ld(’equi3’) AUTO>r(c=’vertical.3.1’,s=’vertical.3.0’)

AUTO>sv(’vertical.3.1’)

AUTO>plot(’vertical.3.1’)

0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95

3.4

3.6

3.8

4

4.2

4.4

4.6

4.8

5

5.2

µ

L2−NORM

(µ = 0.803)

(µ = 0.775)

SOLUCIÓN I

SOLUCIÓN III

SOLU

CIÓ

N II

HBLP

RAMA 1

HB

LP RAMA 2

Figura 3.22: Vertical trazada para ν = 0,163.

En la Figura 3.22, podemos observar el resultado obtenido al representargraficamente la vertical de valor ν = 0,163. La importancia de este graficoradica en el parametro µ, y el haber tomado como eje de ordenadas la normaes debido a que si hubieramos representado el parametro ν en su lugar la curva


se hubiera solapado, y no habrıamos visto toda la informacion que podemosextraer de esta figura. De igual forma podrıamos haber representado como ejevertical cualquiera de los angulos ϕ o θ, sin embargo, el que mayor claridadde grafico nos da es la norma. Aclarado el significado de los ejes coordenados,pasaremos a comentar la grafica en cuestion.

En primer lugar, en la Figura 3.22, podemos distinguir tres solucionesseparadas por dos puntos LP:

I. La solucion que existe entre el eje µ = 0 y la Rama 1 de la curva LP(aunque en el grafico no se haya representado, la solucion I termina enel eje µ = 0).

II. La solucion que existe entre las dos ramas de la curva LP.

III. La solucion que existe desde la Rama 2 de la curva LP en adelante.

Como habıamos dicho anteriormente, la existencia de dos ramas en lacurva de la LP implicaba la existencia de tres soluciones. Las dos primerasestan acotadas, sin embargo, la tercera continua aumentando al crecer elparametro µ. En un apartado posterior, haremos un corte horizontal a µconstante, y veremos si existe esta solucion para valores de ν mayores que launidad.

Por otra parte, hemos conseguido lo que pretendıamos, ya que hemosobtenido dos puntos HB, uno en el equilibrio II y otro en el equilibrio III,a partir de los cuales podremos calcular las bifurcaciones de Hopf en dichosequilibrios.

Bifurcacion de Hopf de la solucion II.

Para hallar la bifurcacion de Hopf de la solucion II, partiremos del puntoHB que hemos encontrado para µ = 0,803 y ν = 0,163.

Creamos pues un nuevo fichero llamado ‘c.Hopf.2.0’, cuyas principalescaracterısticas son las siguientes:

IRS=193 Define la etiqueta del punto correspondiente a la vertical conν = 0,163 que vamos a continuar.

ICP= 0 2 Define como primer parametro de continuacion a µ, y como se-gundo a ν.

ISW=2 Indica que la continuacion se hara en dos parametros, en este casoen µ y ν.


NPR=1 AUTO sacara por pantalla todas las iteraciones realizadas.

Como hemos hecho en ocasiones anteriores a lo largo de este capıtulo,utilizamos el fichero terminado en cero para llegar hasta un punto final dela curva, en este caso el punto HZ. A partir de aquı, creamos otro ficheroterminado en uno que comenzara en este punto y llegara hasta el final dela curva. Este nuevo fichero es ‘c.Hopf.2.1’, y representa la curva de Hopfpara la solucion II. En la Figura 3.23 podemos ver representada la curva deHopf junto con las dos ramas de la curva LP que limitan los equilibrios de lasolucion II.

0.12 0.14 0.16 0.18 0.2 0.22 0.24 0.26 0.28 0.3 0.32

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

ν

µ

TB

HZ

C

CURVA DE HOPF

Figura 3.23: Curva de Hopf para la solucion II.

Una vez hallada la curva de Hopf de la solucion II, haremos un estudiodel espectro de autovalores a lo largo de esta curva, la cual comenzara en elpunto HZ y acabara en el punto TB.

En la Figura 3.24, hemos representado el espectro de autovalores del puntoHZ, del cual partiran las dos bifurcaciones de Hopf, la de la solucion II y lade la solucion III.


Im

Re1

2

4

3

Figura 3.24: Espectro de autovalores en el punto Hopf-Zero.

En al Figura 3.25, hemos hecho un grafico representativo del movimientode los autovalores a lo largo de la curva de Hopf de la solucion II. En elpodemos observar como dichos autovalores van variando su posicion hastaalcanzar el punto TB, el cual es una especie de punto de Hopf degenerado,ya que la pareja conjugada se une para dar un doble cero.

4

2

Im

Re13 4

2

PUNTO TB

Im

Re3 1

CURVA HOPF

Figura 3.25: Espectro de autovalores de la curva de Hopf perteneciente a lasolucion II.


Bifurcacion de Hopf de la solucion III.

Para calcular la curva de Hopf completa de la solucion III, partiremos delpunto de bifurcacion de Hopf (HB) calculado en el corte vertical mostrado enla Figura 3.22. Las coordenadas de este punto son µ = 0,775 y ν = 0,163, ypara continuarlo, creamos un fichero llamado ‘c.Hopf.3.0’ que, como en el casoanterior, nos servira para detectar el punto HZ y tomarlo como comienzo dela continuacion en un segundo fichero que nos dara la curva de Hopf completa.

Una vez alcanzado el punto HZ en la respuesta de AUTO al fichero‘c.Hopf.3.0’, creamos el segundo fichero ‘c.Hopf.3.1’ y lo cargamos de nuevoen AUTO, obteniendo la curva de Hopf que se muestra en la Figura 3.26.

0 0.05 0.1 0.15 0.2 0.25 0.30

0.2

0.4

0.6

0.8

1

1.2

ν

µ

HZ

CURVA DE HOPF

RAMA 2 CURVA LP

Figura 3.26: Curva de Hopf para la solucion III.

Como podemos ver, en la Figura 3.26, solo hemos representado la RAMA2 de la curva LP. Esto es debido a que esta rama es la unica que limita a lasolucion III, mientras que la RAMA 1 es la que marca el lımite de coexistenciade las soluciones I y II.

Vamos a ver como varıan los autovalores a lo largo de esta curva de Hopf.En la Figura 3.24, representamos anteriormente los autovalores del punto HZ


en el cual comienza la curva. A partir de ese instante, los autovalores cambiansu posicion como indica la Figura 3.27, de tal manera que el autovalor queestaba en el cero pasa a la parte real negativa hasta unirse con el autovalor3 y formar una pareja conjugada. En esta ocasion sı podemos afirmar queestamos ante una curva de Hopf estable, ya que todos los autovalores tienenparte real negativa o, al menos, no positiva.

4

2

Im

Re

CURVA HOPF

13

4

2

Im

Re

CURVA HOPF

3

1

Figura 3.27: Espectro de autovalores de la curva de Hopf perteneciente a lasolucion III.

En ambas curvas de Hopf correspondientes a las soluciones II y III, pode-mos ver la importancia que tienen dichos puntos, ya que cuando una parejade autovalores conjugados pasa por el eje imaginario, hay una inestabilidadprovocada por dos autovalores positivos. En el caso de la curva de Hopf dela solucion II, el autovalor que se encontraba en el cero y que designaba lacurva LP, paso a la parte real positiva, convirtiendo en inestable la curva deHopf. Sin embargo, en el caso de la solucion III, el autovalor cero paso a laparte real negativa, lo cual confirio a esta curva la estabilidad.

Por ultimo, antes de acabar este apartado de continuacion de las curvas deHopf, mostramos en la Figura 3.28 la grafica completa de las tres soluciones ysenalaremos en la misma el corte vertical correspondiente al parametro ν convalor 0,163 realizado en este mismo apartado, para que adquiera sentido laFigura 3.22, donde pudimos ver dos puntos LP correspondientes a las ramas1 y 2 de la curva LP, y dos puntos de bifurcacion de Hopf, correspondientesa las soluciones II y III.


0.1 0.12 0.14 0.16 0.18 0.2 0.22 0.24 0.26

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

ν

µ

LP

LP

HB

HBν

= 0.

163

Figura 3.28: Corte vertical con ν = 0,163.

3.3.5. Estabilidad e inestabilidad. Espectro de autova-lores.

En este apartado, estudiaremos la estabilidad e inestabilidad de las tressoluciones que hemos encontrado. Para ello, nos basaremos en el estudiodel espectro de autovalores dentro del espacio de cada una de las solucionesy, concretamente, para cuatro cortes horizontales (µ = constante) que, anuestro entender, son los mas significativos.

El hecho de variar la relacion de brazos (ν = b`) dejando fija la frecuencia

de giro (µ =

√g`

ω), se debe a que debido a la forma de nuestra curva LP, es

mas facil encontrar las tres soluciones en un corte horizontal para cualquierrango de velocidades, que en un corte vertical, donde nos tendrıamos quecenir a intervalos mucho mas pequenos.

Una vez justificado el motivo por el cual tomamos valores de µ constantesy de ν variables, y no viceversa, pasamos a describir las implicaciones de cadauno de los cortes mencionados.

En la Figura 3.29 se muestra una grafica del plano de bifurcaciones con


los cuatro cortes a µ constante.

0.1 0.2 0.3 0.4 0.5 0.6 0.7

0.3

0.4

0.5

0.6

0.7

0.8

0.9

µµ = 0.9

µ = 0.69

µ = 0.58

µ = 0.29

ν

Figura 3.29: Cortes horizontales para valores de µ constantes.

Como en apartados anteriores ya mostramos el espectro de autovalores enlas curva LP, en esta ocasion iremos mostrando la evolucion de los autovaloresa lo largo de cada uno de estos cortes, que a su vez, recorren las tres solucionesque estamos tratando.

Variacion del parametro ν con µ = 0,29.

El primer corte que vamos a realizar corresponde a un valor de µ de 0.29,y podemos verlo en una perspectiva general en la anterior Figura 3.29. Estecorte no interfiere en ninguna de las curvas de Hopf, ni la de la solucion II,ni la de la solucion III, con lo cual lo unico que veremos seran los dos puntosLP que separan a los tres equilibrios.

En la Figura 3.30, mostramos el corte representando el parametro ν frentea la norma. En el podemos ver de izquierda a derecha la primera solucion, queva desde cero hasta que se encuentra el LP de la RAMA 1, la segunda solucionque se encuentra entre las dos ramas de LP, y la tercera, que comienza en


el LP de la segunda rama y continua aumentando el valor de ν hasta que seencuentre con una solucion de tipo 1 como la que representaba la Figura 3.2.De todas ellas, la unica solucion estable es la tercera, lo cual demostraremosviendo el espectro de autovalores.

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

3.5

4

4.5

5

5.5

6

ν

LP RAMA 2

LP RAMA 1 SOLUCIÓN I

SOLUCIÓN II

SOLUCIÓN III

L2−NORM

ESTABLE

Figura 3.30: Corte horizontal para µ = 0,29.

En la Figura 3.31, hemos representado la evolucion de los autovalores alo largo del corte horizontal que estamos tratando. Concretamente lo hemosdividido en cinco figuras numeradas con numeros romanos del uno al cinco yque, a nuestro entender son lo suficientemente significativas. Vamos a explicarcada una de ellas:

I. Nos encontramos en la primera de las tres soluciones, y tenemos dosautovalores reales a la izquierda, y otro dos reales a la derecha quecrean la inestabilidad. Los cuatro evolucionan buscando el cruce de losejes, es decir, el cero. Esta solucion permanece cualitativamente igualpara las tres primeras soluciones, ası que no volveremos a hablar deella.

II. Aquı representamos el LP de la primera rama, en el que el autovalor 1


ha llegado a cero y el resto continuan aproximandose al mismo. Estepunto representa el final de la primera solucion y el comienzo de lasegunda.

III. A lo largo de la segunda solucion, el autovalor 1, que se encontraba encero, se hace real negativo y se va acercando al autovalor 2 hasta quese solapan. Llegados a este punto, ambos autovalores se convierten enuna pareja conjugada y se van separando del eje real. En cuanto a losotros dos autovalores, el 3 se va acercando al cero lentamente, mientrasque el 4 lo hace desde la derecha de forma mas rapida.

IV. Estamos en el LP de la segunda rama, y el autovalor 4 ha llegado alcero. Ademas tenemos la pareja conjugada en la parte real negativa yun cuarto autovalor en el semieje real negativo.

Im

Re23 1 4

Im

Re4

1

2

3

Im

Re

1

2

3 4

Im

Re

3

4

2

1

Im

Re3 2 1 4

I II

IVIII V

Figura 3.31: Espectro de autovalores en el corte horizontal con valor µ = 0,29.

V. Estamos en la solucion III y los autovalores 3 y 4 se han convertidoen una pareja conjugada a la izquierda del eje imaginario, con lo cualestamos ante una solucion estable. Si nos fijamos, la situacion de es-tos autovalores es similar a la de los equilibrios de tipo 1 presentadosal principio de este mismo capıtulo, luego podemos afirmar que estasolucion es heredera de aquella.



En la Figura 3.29 podemos observar como este corte incluye en su reco-rrido la curva de Hopf de la solucion II. En concreto, la corta dos veces, locual indica que una pareja de autovalores conjugados pasara dos veces por eleje imaginario.

En la Figura 3.32 representamos la norma frente al parametro ν, y pode-mos distinguir de nuevo las tres soluciones, aunque esta vez, en la solucionII existen dos puntos HB que alteraran el comportamiento con respecto alprimer corte situado para un valor inferior del parametro µ.

0.1 0.2 0.3 0.4 0.5 0.6

3.5

4

4.5

5

5.5

6

LP RAMA 2

LP RAMA 1

HB(ν = 0.186)

SOLUCIÓN I

SOLUCIÓN III

HB(ν = 0.225)

SOLUCIÓN II

ESTABLE

L2−NORM

ν


En cuanto a la representacion del espectro de autovalores, en esta ocasionsolo vamos a representar lo sucedido en la segunda y la tercera solucion, yaque la situacion de las solucion I es cualitativamente la misma que en elcorte anterior, y puesto que no le estamos dando valores numericos a losautovalores, no merece la pena volver a representarla. Dicho esto, pasemosa analizar la Figura 3.33 en la que solo hemos representado el espectro deautovalores de la soluciones II y III, por las razones dadas anteriormente.


IV V

Im

Re

3

4

Im

Re

III

Im

Re4

2

1

3

2

1

3 4

2

1

Im

Re23 1 4

Im

Re

1

2

3 4

III


I. Este diagrama corresponde al punto LP de la RAMA 1, y separa lasolucion I de la solucion II. En el, tenemos dos autovalores en el semiejereal negativo, uno en el cero y el ultimo en el semieje real positivo (esel que provoca la inestabilidad).

II. Los autovalores 1 y 2, despues de formar un autovalor doble en el se-mieje negativo, se convierten en una pareja de autovalores conjugadoscuya coordenada imaginaria va aumentando en valor absoluto. Los au-tovalores 3 y 4 siguen aproximandose al cero.

III. En este diagrama, observamos como la pareja de autovalores conjugadosha pasado a la parte real positiva, es decir, hemos atravesado la curvade Hopf, ya que la pareja ha pasado por cero. Los otros dos autovaloressiguen aproximandose al cero cada uno desde una parte del eje real.

IV. Aunque aquı mostramos el LP de la RAMA 2, implıcitamente ya hemospasado por el segundo HB de la solucion II, ya que, como podemosobservar, la pareja de autovalores ha vuelto a pasar a la parte realnegativa. Despues del HB, lo que sucede, es que el autovalor 4 llega alcero, y termina la solucion II para este corte, dando paso a la solucionIII.


V. Estamos en la solucion III y los autovalores 3 y 4 se han convertidoen una pareja conjugada a la izquierda del eje imaginario, con lo cualestamos ante una solucion estable.

Antes de pasar al siguiente corte horizontal, vamos a mostrar el corte dela Figura 3.32 sustituyendo la L2-NORM, representada en dicha figura enel eje de ordenadas, por el angulo θ (ver Figura 3.34).

0.2 0.4 0.6 0.8 1 1.2 1.4

3.5

4

4.5

5

5.5

ν

θ

LPRAMA 2

LPRAMA 1


Lo interesante de la Figura 3.34, en la que se ha representado el anguloθ frente al parametro ν, es como enlazan los tres equilibrios variando elparametro θ desde su valor en la solucion I en torno a los π radianes hastala solucion III, cuyo valor del mismo angulo esta entorno a los 2π radianes.

Ademas, podemos apreciar como en la grafica hemos representado valoresdel parametro ν superiores a la unidad, lo cual nos indica que hemos pasadode un equilibrio de los denominados en el capıtulo anterior de tipo III a unode tipo I recorriendo todo el rango del angulo θ para ello.



Este corte quizas sea el mas interesante de todos, ya que, ademas deincluir las tres soluciones, corta las dos curvas de Hopf de las soluciones II yIII (ver Figura 3.29).

En la Figura 3.35 representamos la norma frente al parametro ν, y pode-mos distinguir de nuevo las tres soluciones, aunque esta vez, en la solucionII existe un HB y en la solucion III existe otro.

0.1 0.2 0.3 0.4 0.5 0.6

3.5

4

4.5

5

5.5

6

ν

L2−NORM

LP RAMA 1

LP RAMA 2

HB(ν = 0.210)

HB(ν = 0.173)

SOLUCIÓN I

SOLU

CIÓ

N II

SOLUCIÓN III

ESTABLE


En cuanto a la representacion del espectro de autovalores, vamos a repre-sentar lo sucedido en la segunda y la tercera solucion, ya que la situacion delas solucion I es cualitativamente la misma que en el primer corte. Dicho esto,pasemos a analizar la Figura 3.36 en la que hemos representado el espectrode autovalores de la soluciones II y III.

I. Este diagrama corresponde al punto LP de la RAMA 1, y separa lasolucion I de la solucion II. En el, tenemos dos autovalores en el semiejereal negativo, uno en el cero y el ultimo en el semieje real positivo (esel que provoca la inestabilidad).


Im

Re23 1 4

Im

Re

1

2

3 4

III

IV V

Im

Re

3

4

Im

Re

III

Im

Re

2

1

3

2

1

4 3 4

2

1


II. Los autovalores 1 y 2, despues de formar un autovalor doble en el se-mieje negativo, se convierten en una pareja de autovalores conjugadoscuya coordenada imaginaria va aumentando en valor absoluto. Los au-tovalores 3 y 4 siguen aproximandose al cero.

III. En este diagrama, observamos como la pareja de autovalores conjuga-dos ha pasado a la parte real positiva, es decir, hemos atravesado porla curva de Hopf, ya que la pareja ha pasado por cero. Como el auto-valor 4 esta en el cero, esto implica que estamos en el LP que separalas soluciones II y III.

IV. Aquı mostramos el HB de la curva de Hopf de la solucion III. Podemosver como la pareja de autovalores conjugados 1 y 2 se encuentran sobreel eje imaginario y como los autovalores 3 y 4 se van aproximando paraformar una segunda pareja conjugada.

V. Estamos en la solucion III y los autovalores 3 y 4 se han convertidoen una pareja conjugada a la izquierda del eje imaginario, con lo cualestamos ante una solucion estable.



En este corte ya solo podemos ver una unica solucion, y es la III. En laFigura 3.29 observamos como en el corte se pasa por la curva de Hopf de lasolucion III.

En la Figura 3.37 representamos la norma frente al parametro ν, y pode-mos distinguir una unica solucion que solo es estable a partir de la curva deHopf.

0.1 0.2 0.3 0.4 0.5 0.6 0.7

4

4.5

5

5.5

6

ν

L2−NORM

HBHB(ν = 0.133)

SOLUCIÓN III

ESTABLE


En cuanto a la representacion del espectro de autovalores, vamos a repre-sentar en la Figura 3.38, lo sucedido a lo largo de este corte antes y despuesde la curva de Hopf.

I. Partimos de los cuatro autovalores situados dos a cada lado del ejeimaginario y todos sobre el eje real. Los cuatro se van acercando alcero.

II. El autovalor 2 se acerca al cero mas rapido que el 1, y ello provocaque ambos se conviertan en un autovalor doble, y de ahı a una parejaconjugada en la parte real positiva.


4

3

4

3

Im

Re3

Im

Re

III

IV V

Im

Re

3

4

Im

Re

III

Im

Re

2

1

2

1

2

1

14 2 3 4

1

2


III. Al igual que sucedio en el diagrama anterior para el caso de los auto-valores 1 y 2, el 3 y el 4 forman otra pareja conjugada, aunque esta vezen la parte estable del diagrama.

IV. Alcanzamos el punto HB de Hopf, ya que la pareja de autovalores queeran inestables, llegan al eje imaginario.

V. Por ultimo, alcanzamos la posicion estable, donde los cuatro autovaloresforman dos parejas conjugadas en la parte real negativa

3.4. Conclusiones sobre la continuacion numeri-

ca de los equilibrios.

Una vez estudiados los cuatro cortes que, a nuestro entender, son los massignificativos, haremos una serie de reflexiones:

La solucion I siempre es inestable, ya que en todos los cortes permane-cen dos autovalores en la parte real positiva.


La solucion II siempre es inestable, aunque si midieramos el grado deinestabilidad, hay zonas donde solo tiene un autovalor en la parte realpositiva y otras en las que tiene tres.

La solucion III es, en casi todo su rango, estable. Si volvemos a laFigura 3.26, despues de haber realizado el estudio de los autovaloresque afectan a la misma, podemos afirmar que todos los puntos con valordel parametro µ inferior al que corresponde al punto HZ y con valordel parametro ν superior al determinado por la rama 2 de la curva LP,son siempre estables, y de la misma forma, todos los puntos situados ala derecha de la curva de Hopf de este equilibrio tambien lo son, siendoel resto de equilibrios (los que se encuentran entre la curva de Hopf yla rama 2 de la curva LP) inestables. Resumiendo, la lınea que separaa los equilibrios estables de los inestables es la curva LP por debajo delpunto HZ, y la curva de Hopf por encima del mismo punto.

Capıtulo 4

Continuacion numerica deorbitas periodicas.

4.1. Introduccion.

En el capıtulo anterior, estudiamos la estabilidad e inestabilidad del sis-tema de la Figura 2.1 para todos los puntos de equilibrio. En este capıtulo,lo que pretendemos averiguar son las posibles estabilidades que se den enorbitas periodicas cuyos orıgenes son los puntos de equilibrio hallados an-teriormente. Para ello, tomaremos como origen de las orbitas periodicas lospuntos de Hopf que aparecen en la Figura 4.1.

4.2. Algunas nociones sobre AUTO2000.

Antes de comenzar a calculas las orbitas periodicas a partir de los puntosHB mostrados en la Figura 4.1, daremos algunas nociones basicas de comofuncionan estas en AUTO2000.

En primer lugar analizaremos los ficheros de tipo ‘x.ccc’. Para ello, toma-remos uno de ejemplo:


2 2 10 NICP,(ICP(I),I=1 NICP)


218 0 100 0 100 NMX,RL0,RL1,A0,A1





66

CAPITULO 4. CONTINUACION NUMERICA DE ORBITASPERIODICAS. 67



En este fichero podemos observar tres diferencias fundamentalmente conrespecto a los ficheros de equilibrio:

El valor de la variable IPS ha cambiado a 2 para orbitas periodicas.

El valor de la variable ISP tambien cambia a 2 para orbitas periodicas.

El vector ICP debe contener al PAR[10], ya que este simboliza alperıodo.

0.1 0.12 0.14 0.16 0.18 0.2 0.22 0.24 0.26 0.28

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

ν

µ

µ = 0.9

µ = 0.69

µ = 0.58

HB3

HB22

HB11

HB21

HB12

Figura 4.1: Puntos de Hopf a partir de los que se continuaran las orbitasperiodicas.

El resto de las variables cambian los valores igual que en el caso de con-tinuacion de equilibrios, es decir, IRS establece el valor de la etiqueta acontinuar, ISW marca el numero de parametros a continuar, etc. . . salvo lavariable DS, cuyo signo ahora no tiene ninguna importancia, ya que soloexiste una orbita periodica.


Por otra parte, el resultado obtenido por pantalla desde la consola de AU-TO no es igual que para los equilibrios, ya que ahora en lugar de devolver losvalores de las cuatro variables independientes, devuelve los valores maximosque alcanzan estas en cada iteracion. A continuacion mostramos parte de unfichero de bifurcaciones ‘b.xxx’:

L2-NORM MAX(1) MAX(2) PERIOD

5.00878E+00 6.91462E-01 4.85899E+00 6.34414E+00

5.00879E+00 6.95850E-01 4.86143E+00 6.34409E+00

5.00884E+00 7.02394E-01 4.86515E+00 6.34359E+00

En nuestro caso particular, L2-NORM representa la amplitud de la orbi-ta, MAX(1) y MAX(2) los valores maximos de ϕ y θ, respectivamente, yPERIOD el perıodo de la orbita.

Por ultimo, conviene saber que, en las orbitas periodicas, la estabilidadno viene marcada por los autovalores, sino que existen unos valores similaresa estos llamados multiplicadores, y establecen la estabilidad siguiendo lassiguientes reglas:

Trazar en el plano complejo una circunferencia de radio unidad centradaen el origen.

Dibujar los multiplicadores segun sus coordenadas reales e imaginarias.

Un multiplicador valdra siempre 1 y, si los otros tres estan en el interiorde la circunferencia, estamos ante una orbita estable.

Si alguno de los cuatro multiplicadores quedara fuera de la circunferen-cia, estarıamos ante una orbita inestable.

Establecidas ya unas pautas iniciales para manejar AUTO con orbitasperiodicas, comenzaremos la continuacion de las mismas a partir de los puntosHB marcados en la Figura 4.1.

4.3. Continuacion de orbitas periodicas a par-

tir de puntos de Hopf.

Los puntos de Hopf que vamos a continuar en este apartado, vienen dadospor los tres cortes a µ constante que aparecen en la Figura 4.1. En cada unode los siguientes apartados, mostraremos, para cada uno de los cortes, lasorbitas periodicas obtenidas, ası como un diagrama de sus multiplicadoresque nos indicaran la estabilidad de dichas orbitas.


4.3.1. Continuacion de los puntos de Hopf contenidosen la horizontal de valor µ = 0,58.

Como en el capıtulo anterior ya mostramos la Figura 3.32 con el cortecompleto de la horizontal µ = 0,58, mostraremos ahora unicamente la partede esa figura que nos interesa, y que se encuentra entre los dos puntos deHopf HB11 y HB12. En la Figura 4.2 podemos apreciar la orbita periodicaresultante de continuar el punto HB12.

0.14 0.16 0.18 0.2 0.22 0.24 0.26

4.1

4.2

4.3

4.4

4.5

4.6

4.7

L2−NORM

ν

HB11

HB12

ÓRBITA PERIÓDICA

PD

SOLU

CIÓ

N II

Figura 4.2: Orbita periodica correspondiente a µ = 0,58.

Como podemos observar, partiendo del punto HB12, hemos continuadola orbita hasta llegar al punto HB11.

Tambien aparece en la Figura 4.2 un punto PD de orbita periodica, el cualpodrıamos continuar para obtener una curva PD de orbitas periodicas. Sinembargo, en este proyecto, nos limitaremos a estudiar la estabilidad de lasorbitas periodicas que obtengamos a partir de los puntos de Hopf unicamente.

A continuacion estudiaremos la estabilidad de la orbita periodica a partirde sus multiplicadores. Para ello, en la Figura 4.3 hemos dibujado la circun-ferencia de radio unidad con los multiplicadores mas representativos de la


orbita periodica.

Im

Re12 4.13.1

4.2

3.2

3.3

4.3

3.5

4.5 4.4

3.4

Figura 4.3: Multiplicadores para la orbita periodica con µ = 0,58.

En la Figura 4.3, hemos representado los cuatro multiplicadores, de loscuales el numero 1, siempre se encuentra en la coordenada 1 del eje real posi-tivo, el 2 apenas varıa su posicion, y los otros dos son los que mas se mueven.Concretamente, para los multiplicadores 3 y 4 mostramos en la grafica doslıneas de colores diferentes que indican sus distintas posiciones. Al principiolos dos multiplicadores se encuentran a ambos lados de la circunferencia, has-ta que se unen fuera de ella y la van rodeando (posiciones 3.2 y 4.2). Llegaun momento en que se vuelven a unir formando un multiplicador doble (3.3y 4.3) para despues separarse cada uno en una direccion. El punto PD dela Figura 4.2, se da para las posiciones 3.4 y 3.5, cuando el multiplicador 3llega a la circunferencia. A partir de ahı, el multiplicador 4 se va haciendocada vez mas grande, el multiplicador 2 mas pequeno y el 3 se queda dentrode la circunferencia en el semieje real negativo.

Al repasar el movimiento de los multiplicadores, observamos como noexiste ningun punto de la orbita que tenga todos los multiplicadores en elinterior de la circunferencia, luego esta orbita nunca llegara a ser estable.


4.3.2. Continuacion de los puntos de Hopf contenidosen la horizontal de valor µ = 0,69.

El corte horizontal con valor de µ igual a 0,69 lo podemos ver representadoen la Figura 4.1 como el parametro µ frente a ν, o en la Figura 3.35 en la queel eje de abscisas representa el valor de ν pero el de ordenadas nos proporcionalos valores de la norma.

Una vez mostrado el corte en varios ejes de coordenadas, vamos a cen-trarnos en la orbita periodica cuyo origen es el punto HB22, pertenecientea la solucion III, y cuyo final es el punto HB21, perteneciente a la solucionII (ver Figura 4.4).

0.1 0.15 0.2 0.25

3.8

4

4.2

4.4

4.6

4.8

5

ν

L2−NORM

SOLUCIÓN II

SOLUCIÓN III

LP

HB22

HB21

ÓRBITA PERIÓDICA

PD2

LP PD1

O. P. ESTABLE


En esta ocasion, en el punto HB del que partimos, coinciden dos ramasde equilibrios con distinta estabilidad, es decir, la que proviene de la solucionIII es estable, y la que proviene de la solucion II es inestable, luego, a priori,no sabrıamos si cerca del equilibrio, la orbita periodica es estable o inestable.Para saberlo, hay que hacer un estudio de los multiplicadores en dicha orbitaperiodica, y comprobar la estabilidad de la misma. El resultado de dicho


estudio lo podemos ver en la Figura 4.5.

2 13

22

2

33

3

Im

Re

Im

Re2 3 1

III

Im

Re3

Im

Re2 3

III IV

2 1 1


La Figura 4.5 la hemos dividido a su vez en 4 figuras numeradas comoI, II, III y IV. En todas ellas hemos obviado el multiplicador que siemprese encuentra en el semieje real positivo en la coordenada 1. Cada una de lascuatro figuras simboliza lo siguiente:

I. Esta posicion , corresponde al principio de la orbita periodica, en elpunto HB22. En ella vemos como los tres multiplicadores se encuentrandentro de la circunferencia de radio unidad, luego la orbita es estableen ese punto. A partir de ahı, el multiplicador 1 se mueve hacia el cero,y los multiplicadores 2 y 3 se unen formando una pareja conjugada


que se va desplazando hacia el eje imaginario para terminar de nuevoen el eje real, aunque, esta vez, en la parte negativa del mismo. Apartir de este momento, el multiplicador 2 se mueve hacia el borde dela circunferencia por su parte negativa, y el 3 se dirige al cero.

II. En esta figura se representa el primer punto de duplicacion de perıodo,llamado PD1 en la Figura 4.4. Este punto se caracteriza porque el mul-tiplicador 2 esta saliendo por la parte real negativa de la circunferenciay, en nuestro caso, porque hace que nuestra orbita se haga inestable apartir de este punto. Por otra parte, podemos observar como el multi-plicador 3 se va acercando lentamente al cero, y el 1 se va desplazandohacia la derecha buscando el borde de la circunferencia.

III. La transicion entre las figuras II y III, refleja como el autovalor 2 cambiade sentido y se dirige de nuevo a la circunferencia, aunque antes dellegar a esta, sera el multiplicador 1 el que la alcance por su parte realpositiva. Llegados a esta situacion (III), estamos ante un punto lımitede orbitas periodicas, denominado en la Figura 4.4 LP, y que nos dejaun segundo multiplicador fuera de la circunferencia de radio unidad.

IV. Por ultimo, representamos en esta figura el punto de duplicacion deperıodo PD2, en el que podemos ver como el multiplicador 2 vuelvea entrar por la parte real negativa dentro de la circunferencia. Sinembargo, al estar el multiplicador 1 fuera de la misma, la orbita siguesiendo inestable hasta llegar al punto HB21, donde termina.

Mostrado el espectro de los multiplicadores del corte horizontal que esta-mos tratando, podemos afirmar que en el punto HB22, la orbita periodicaderiva de la parte de la solucion III que es estable, y que dicha estabilidadsolo se mantiene hasta el punto PD1.

A continuacion, representaremos graficamente nuestros dos grados de li-bertad ϕ y θ con los valores proporcionados por el AUTO para la orbitaperiodica estable. Evidentemente, al ser las dos soluciones periodicas, el re-sultado sera una curva cerrada. El resultado de la representacion grafica, lopodemos ver en la Figura 4.6, aunque con respecto a nuestro sistema, loideal serıa pasar dicha grafica a coordenadas cartesianas adimensionales, pa-ra ası tener una idea mas intuitiva del tipo de orbita estable que describirıanuestro pendulo. Para ello, escribiremos las coordenadas cartesianas localesdel pendulo en funcion de los angulos ϕ y θ. El resultado serıa el siguiente:

x=` · sin ϕ · cos θ

y=` · sin ϕ · sin θ

z=−` · cos ϕ


4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.80.7

0.8

0.9

1

1.1

1.2

1.3

1.4

θ

ϕ

Figura 4.6: Representacion del angulo ϕ frente a θ para la orbita periodicacon µ = 0,69.

Lo unico que resta ahora, es adimensionalizar las coordenadas cartesianas,y para ello, lo unico que haremos sera dividir ambos miembros de las tresecuaciones por `, obteniendo el vector de posicion en coordenadas locales yadimensionalizado:

X=sin ϕ · cos θ

Y=sin ϕ · sin θ

Z=− cos ϕ

Una vez que tenemos las ecuaciones adimensionales que nos definen lascoordenadas cartesianas a partir de los angulos ϕ y θ, simplemente tenemosque hacer una grafica en tres dimensiones que nos represente en los ejescartesianos la orbita periodica estable que representamos en la Figura 4.6en coordenadas esfericas. Esta grafica la podemos ver representada en laFigura 4.7, y en ella vemos como serıa la trazada del pendulo en el caso deesta orbita periodica estable. Lo mas curiosa de ella es, que el parametroque varıa es siempre la relacion de brazos, lo cual no es muy intuitivo, ya


que lo mas razonable serıa variar la velocidad de giro. Sin embargo, como elcorte horizontal del que proviene esta orbita es a µ constante y ν variable, elresultado obtenido es el esperado.

−0.2 −0.15 −0.1 −0.05 0 0.05 0.1 0.15−1

−0.5

0

−0.5

−0.4

−0.3

−0.2

−0.1

0

0.1

0.2

b

X

l

Y

Figura 4.7: Orbita periodica con µ = 0,69 en coordenadas cartesianas.

4.3.3. Continuacion del punto de Hopf contenido en lahorizontal de valor µ = 0,9.

El corte horizontal con valor de µ igual a 0,9 lo podemos ver representadoen la Figura 4.1 como el parametro µ frente a ν, o en la Figura 3.37 en la queel eje de abscisas sigue representando el valor de ν pero el de ordenadas nosproporciona los valores de la norma. Este corte contiene una unica solucionque, como vimos en el capıtulo anterior, solo es estable para valores de νsuperiores al del punto HB.

En la Figura 4.8 podemos ver la orbita periodica obtenida al continuar elpunto HB del corte horizontal que estamos tratando. De nuevo obtenemosun punto de bifurcacion de doble perıodo PD y un punto lımite LP.

Si observamos la rama de la solucion III, podemos ver como la orbitaperiodica continua a la parte inestable de la misma, luego, a falta de estudiarlos multiplicadores, podrıamos decir que la orbita periodica es inestable. Noobstante, haremos, a continuacion, un estudio de los multiplicadores y losrepresentaremos graficamente como en los dos casos anteriores.

A la hora de representar los multiplicadores, hemos omitido el que siemprese encuentra en el semieje real positivo con valor real 1, debido a que estemultiplicador siempre permanece inalterable en esa posicion en las orbitasperiodicas. Dicho esto, en la Figura 4.9 hemos trazado las posiciones mas


0 0.05 0.1 0.15 0.2 0.25 0.3

4.75

4.8

4.85

4.9

4.95

5

5.05

5.1

5.15

ν

HB

ÓRBITA PERIÓDICA

SOLUCIÓN III

LP

PD

L2−NORM


relevantes de los tres multiplicadores restantes y, a continuacion, explicaremosbrevemente cada uno de los esquemas que allı se muestran:

I. Nos encontramos en la posicion inicial desde donde parte la orbitaperiodica. En ella podemos ver que existe una pareja de multipicadoresconjugados en la parte real positiva y dentro de la circunferencia deradio unidad, sin embargo, el otro multiplicador ya se encuentra fuerade la misma en el eje real positivo luego, como ya dijimos en este mismoapartado, la orbita hereda la inestabilidad de la rama de la solucion IIIde la que partimos. La evolucion de los tres multiplicadores la podemosver en la misma figura, en la que el multiplicador 1 tiende a alejarse dela circunferencia, y el 2 y el 3 se dirigen a la circunferencia y al cero,respectivamente.

II. Llegamos a un punto de bifurcacion de doble perıodo, ya que el mul-tiplicador 2 ha alcanzado la circunferencia por la parte real negativa.Mientras, el multiplicador 3 avanza lentamente hacia el cero y el 1 sealeja por el eje real positivo.


III. En esta figura, hemos mostrado el punto lımite de la orbita periodica,en la que el multiplicador 1, tras haber cambiado el sentido en el ejereal, entra en la circunferencia por la parte real positiva. Ademas, elmultiplicador 2 se aleja de la circunferencia y el 3 se sigue acercando acero.

IV. Por ultimo, terminamos con la evolucion de los multiplicadores antes deque finalicen su recorrido. En esta figura podemos ver como el autovalor2 se aleja por la parte real negativa y fuera de la circunferencia, el 3se sigue acercando lentamente al cero, aunque nunca llegara a el, y elmultiplicador 1 entra en la circunferencia y va disminuyendo su valoren el eje real positivo.

1

I

Im

Re3

Im

Re3

III IV

2 1

22

2

33

3

Im

Re

Im

2 3

II

Re1

2 1


Capıtulo 5

Conclusiones.

A lo largo de los tres capıtulos anteriores del proyecto, hemos estudiadoanalıtica y numericamente el sistema objeto de nuestro trabajo, con el ob-jetivo de calcular su estabilidad tanto en posiciones de equilibrio como enorbitas periodicas, por medio de la formulacion lagrangiana.

Figura 5.1: Posicion de equilibrio con el pendulo cruzado.

Fundamentalmente, nos hemos basado en la posicion del pendulo definidapor la Figura 5.1, cuya principal caracterıstica es que la longitud del penduloes mayor que la del brazo rotatorio, lo cual permite que la masa que seencuentra en el extremo del pendulo se situe en el cuadrante opuesto albrazo rotatorio y que la fuerza centrıfuga sea capaz de equilibrar al peso y a

78

CAPITULO 5. CONCLUSIONES. 79

la tension del hilo. Ademas, los tres equilibrios que genera esta posicion, sondebidos a la rotacion del sistema a altas velocidades, ya que de otra formaserıa imposible su existencia y, los unicos equilibrios que se darıan, serıan losdefinidos en las Figuras 5.2 y 5.3.

Debido a que las ecuaciones diferenciales de nuestro modelo son muycomplejas, el estudio analıtico se ha visto muy reducido, y el mayor peso delproyecto se lo ha llevado la parte numerica realizada con AUTO2000.

Con respecto ha dicha parte numerica, en la posicion definida por laFigura 5.1, se han encontrado tres tipos de equilibrio, de los cuales solo unoproduce soluciones estables, tanto de equilibrio como de orbitas periodicas.

Mientras que los dos equilibrios inestables en ningun caso superan el valoruno del parametro adimensional ν = b

`(b representa la longitud del brazo

horizontal rotatorio y, `, la longitud del pendulo), el equilibrio que presen-ta estabilidad en casi todo su rango, tiende a converger hacia la solucionde equilibrio representada en la Figura 5.2, que, por otra parte, siempre esestable, y sı existe para valores del parametro mayores que la unidad.

Figura 5.2: Posicion de equilibrio clasica.

Podemos concluir diciendo que, en el presente proyecto, se han cumplidolos objetivos marcados en el capıtulo de introduccion, ya que hemos calculadonumericamente todas las soluciones de equilibrio posibles de nuestro sistema,y ademas hemos mostrado la estabilidad de una orbita periodica ante laperturbacion de un equilibrio. Ademas, se ha demostrado la capacidad delprograma AUTO para la continuacion de equilibrios y orbitas periodicas enfuncion de uno o dos parametros (velocidad y relacion de brazos), lo cual eraun objetivo implıcito en la realizacion del proyecto.

CAPITULO 5. CONCLUSIONES. 80

Figura 5.3: Posicion de equilibrio con el pendulo invertido.

Bibliografıa

[1] Pozuelo Dıaz, P.: Modelado y simulacion del pendulo esferico deFuruta (Proyecto fin de carrera).Julio 2002

[2] Strogatz, S. H.: Nonlinear Dynamics and Chaos: With Applica-tions in Physics, Biology, Chemistry and Engineering.Addison-Wesley 1994

[3] Roseau, M.: Vibrations in Mechanical system.Springer-Verlag

[4] Ranada, A.: Dinamica Clasica.Alianza Universidad Textos

[5] Rodrıgez Danta M.: Cuadernos de Mecanica Dinamica.E.T.S.I. Universidad de Sevilla.

[6] Doedel, E.; Paffenroth, R.; Champneys, A.; Auto2000: Continuationand bifurcation software for ordinary differential equations.Junio 2002

[7] Cascales, B.; Lucas, P.; Mira, J.M.; Pallares, A.;Hayna I.; Schlegl E.: Unadescripcion de LATEX2.Noviembre 1998

[8] Kopka, H.; Daly, P.W.: A guide to LATEX. Document preparationfor beginners and advanced Users.Edition. Addison.Wesley, 1999.

81

Inestabilidad inducida por rozamiento en un p¶endulo...

Documents

Transcript of Inestabilidad inducida por rozamiento en un p¶endulo...